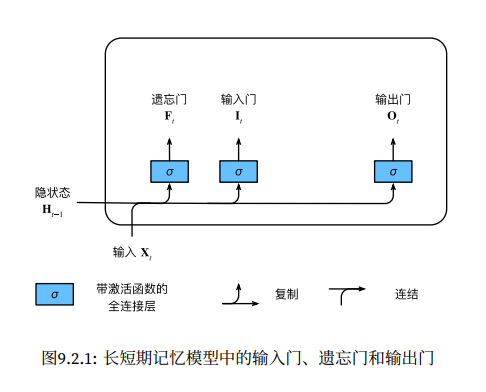
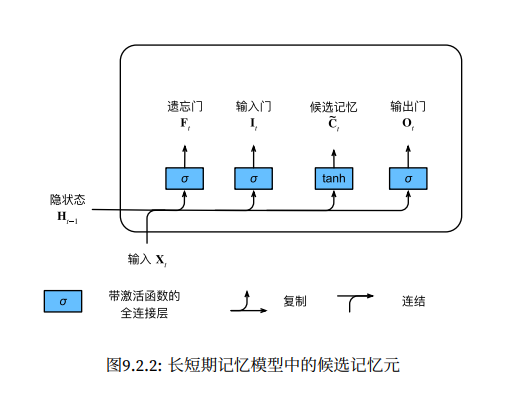
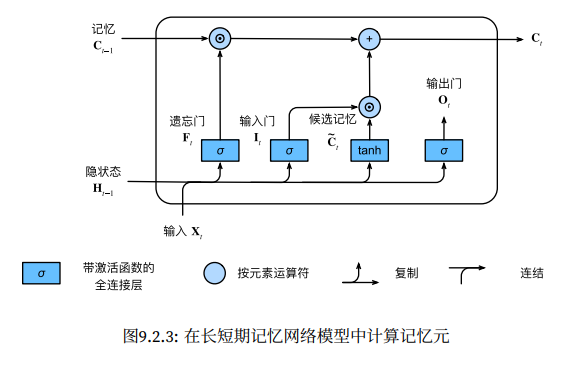
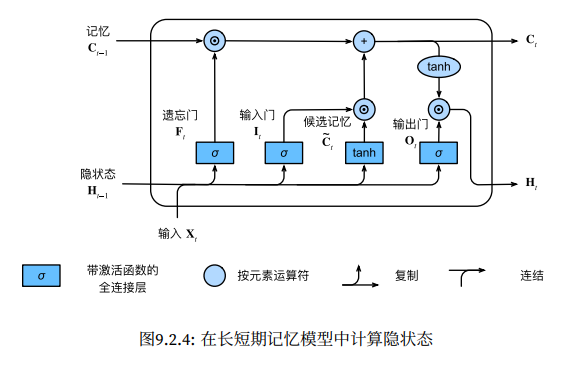
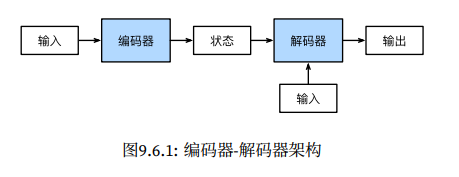
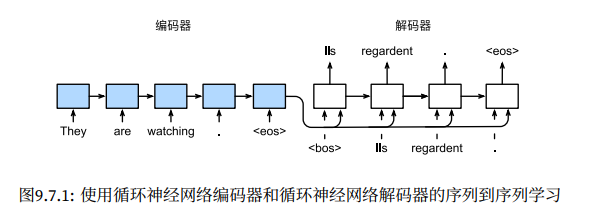
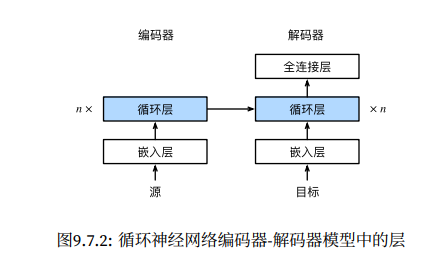
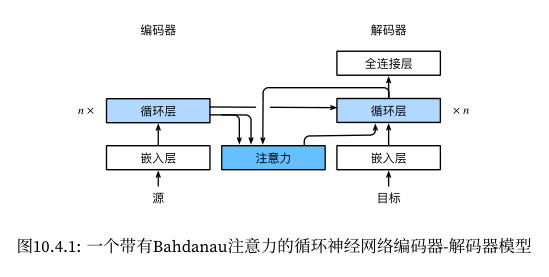
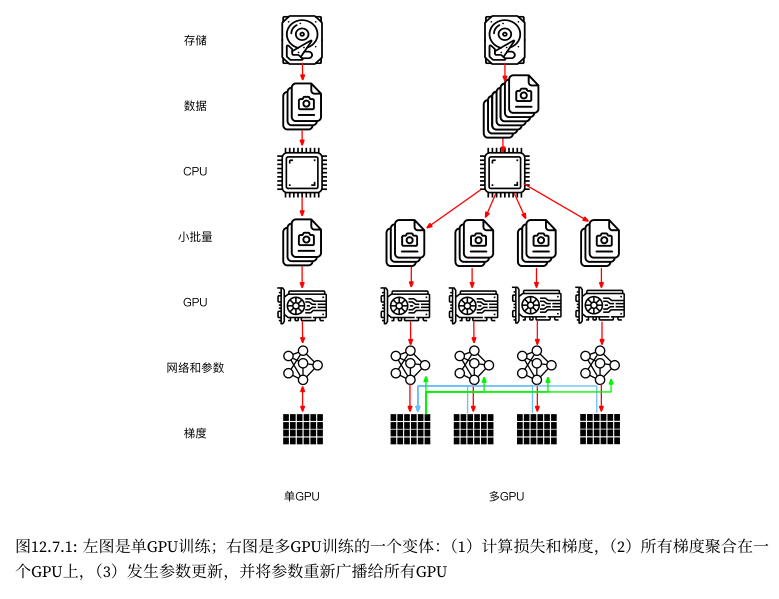
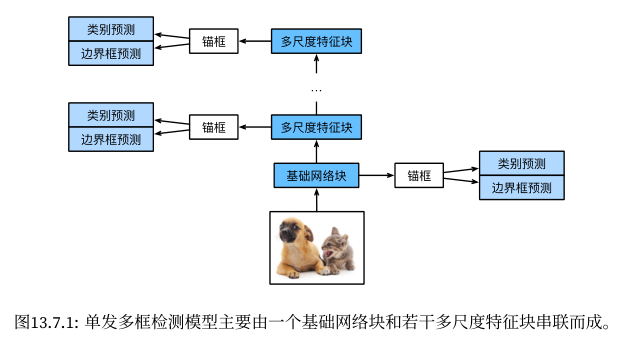
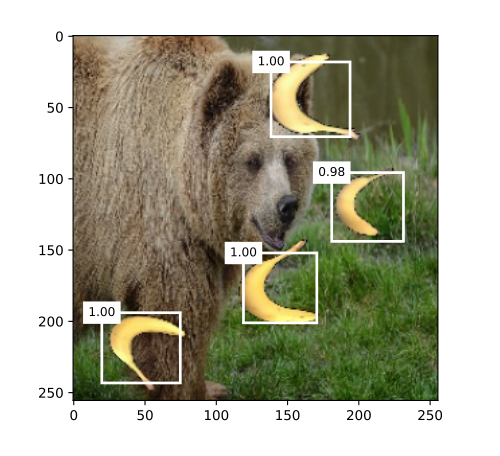
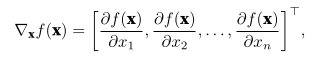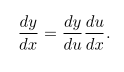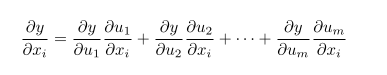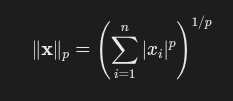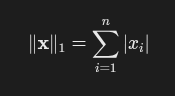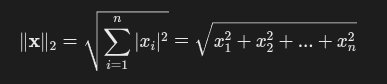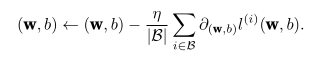引言
日常生活中的机器学习
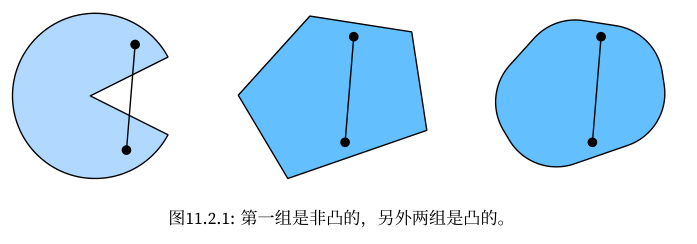
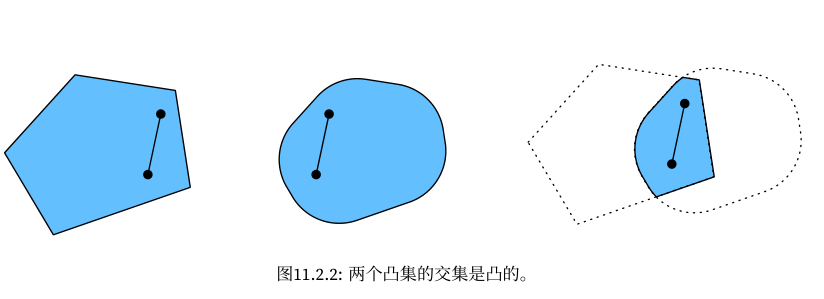
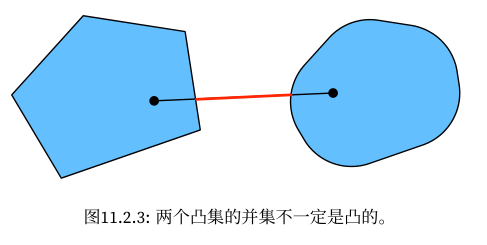
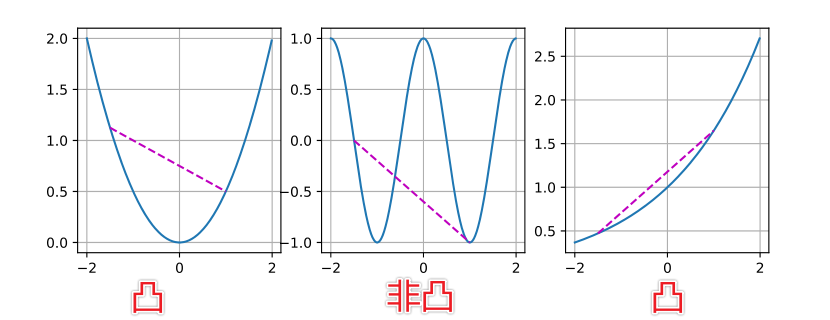
普通编程:编写指令集合,指示机器如何处理数据;
机器学习:提供数据和结果,让机器学习并生成指令集合;
机器学习中的关键组件
核心组件包括:
数据
模型
目标函数:用来判断模型是否合格;
优化算法:调整模型参数的算法;
常用的一种方法是梯度下降,即先按随机的微小幅度,调整参数值。然后观察损失值的变化。如果损失变小,说明微调方向正确。如果损失变大,说明微调方向搞错了。很像猜价格的游戏,张三先随机报个价格,李四反馈高了还是低了。然后张三调整报价,李四继续反馈高了还是低了。最终价格不断向正确价格靠近。
各种机器学习问题
监督学习
常用的问题类型:
回归问题:猜猜有多少(类似填空题)。例如根据各种房屋的属性,猜猜房子值多少钱;根据病人的各种特征,猜猜需要花费多少手术费用;根据各种气象指标,猜猜会下多少雨;
分类问题:猜猜是哪个(类似选择题)。比如识别手写的数字是哪个数字;识别图片中的动物是猫是狗;
标记问题:给项目打标签;例如博客文章的标签、给论文或文献打标签;
搜索:对一组项目按相关性进行排序;
推荐系统:向特定用户推送个性化的内容;
序列学习:本次输出,跟过往的历史输入有关;
无监督学习
常见的问题类型:
聚类
主成分分析:有点像对事物进行抽象,用关键的几个要素,描述事物的状态;
因果关系:发现各数据之间的关系;
GAN:生成式对抗网络
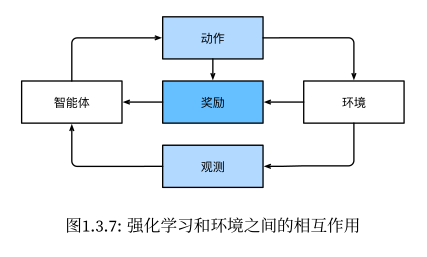
与环境互动
环境是变化的,模型是静态的。如果二者结合起来,让模型不断和环境进行互动,模型便动态化了。
强化学习
设计一个奖励机制,根据模型的输出质量,进行奖励,从而让模型学会什么是好的输出策略。
强化学习是一种通用性很强的框架,这意味着我们也可以将监督学习类型的问题,转成强化学习类型。
预备知识
数据操作
入门
标量:单个数值;
张量:由数值组成的多维数组;
向量:只有一个轴的张量;
矩阵:有两个轴的张量;
1 2 3 tensor([[ 0.7277, -1.3848, -0.2607, 0.9701],
运算符
相同形状的张量,常见的标准算术运算符,都可以用来实现按元素计算。
1 2 3 x = torch.tensor([1.0 , 2 , 4 , 8 ])2 , 2 , 2 , 2 ])
1 2 3 4 5 (tensor([ 3., 4., 6., 10.]),
1 tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
张量支持堆叠,并且可以指定堆叠的轴
1 2 3 X = torch.arange(12 , dtype=torch.float32).reshape((3 ,4 ))2.0 , 1 , 4 , 3 ], [1 , 2 , 3 , 4 ], [4 , 3 , 2 , 1 ]])0 ), torch.cat((X, Y), dim=1 )
1 2 3 4 5 6 7 8 9 (tensor([[ 0., 1., 2., 3.],
逻辑运算符也支持
1 2 3 tensor([[False, True, False, True],
广播机制
按元素计算的前提是两个张量的形状相同,当形状不同时,需要先通过复制的形式扩展张量,让它们具有相同的形状,之前再执行按元素的计算,即所谓的广播机制。
1 2 3 a = torch.arange(3 ).reshape((3 , 1 ))2 ).reshape((1 , 2 ))
1 2 3 4 (tensor([[0],
1 2 3 tensor([[0, 1],
索引和切片
可通过索引的方式,读取或修改张量中的元素
1 2 3 (tensor([ 8., 9., 10., 11.]),
1 2 3 tensor([[ 0., 1., 2., 3.],
通过索引还可以实现批量赋值
1 2 3 tensor([[12., 12., 12., 12.],
节省内存
通常在执行张量运算后,会返回一个新的张量。如果想要就地更新,不返回新张量,则可以使用 [:] 运算符,例如:
1 2 3 4 y = torch.zeros(2 , 3 )1 1
转换为其他 Python 对象
张量和 Numpy 可以相互转换
1 2 3 A = X.numpy()type (A), type (B)
1 (numpy.ndarray, torch.Tensor)
大小为 1 的张量可以直接转换为 Python 标量
1 2 a = torch.tensor([3 ])float (a), int (a)
数据预处理
pandas 是一个常用的数据读取和处理库
读取数据集
模拟创建一个 csv 文件
1 2 3 4 5 6 7 8 9 10 import os'..' , 'data' ), exist_ok=True )'..' , 'data' , 'house_tiny.csv' )with open (data_file, 'w' ) as f:'NumRooms,Alley,Price\n' ) 'NA,Pave,127500\n' ) '2,NA,106000\n' )'4,NA,178100\n' )'NA,NA,140000\n' )
使用 pandas 读取 csv 数据
1 2 3 4 import pandas as pdprint (data)
1 2 3 4 5 NumRooms Alley Price
处理缺失值
有两种处理缺失值的办法,一种是直接删除,一种是插值填充。以下示例用平均值来填充
1 2 3 inputs, outputs = data.iloc[:, 0 :2 ], data.iloc[:, 2 ]print (inputs)
1 2 3 4 5 NumRooms Alley
如果值的类型是离散值,例如类别,那么可以将缺失值 NaN 也视为一种类型进行处理。
pandas 可以自动拆分列,并使用 1 和 0 来标记不同的类别
1 2 inputs = pd.get_dummies(inputs, dummy_na=True )print (inputs)
1 2 3 4 5 NumRooms Alley_Pave Alley_nan
转换为张量格式
如果所有条目都是数值类型,那么即可以转换成张量格式
1 2 3 4 import torch
1 2 3 4 5 (tensor([[3., 1., 0.],
线性代数
标量
标量仅包含一个数值,可由只有一个元素的张量表示。常用数学符号为小写字母,例如 x, y, z
1 2 3 4 5 6 7 import torch3.0 )2.0 )
向量
向量是包含多个标量的数组(列表)。这些标量称为元素或者分量。向量常用数学符号为粗体小写字母 x , y , z
向量可由一维张量来表示:
一般使用列向量作为向量的默认方向,示例如下:
x = [ x 1 x 2 ⋮ x n ]
在数学上,使用
x ∈ R n
表示向量
x
由 n 个实值标量组成。向量的长度也叫做向量的维度。
矩阵
矩阵是二维的张量,通常使用粗体大写字母表示,例如 X , Y , Z
数学符号
A ∈ R m × n
表示矩阵 A 由 m 行和 n 列的实值标量组成。
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] .
1 A = torch.arange(20 ).reshape(5 , 4 )
1 2 3 4 5 tensor([[ 0, 1, 2, 3],
矩阵中的标量可使用符号
[ A ] i j
进行表示
张量
张量由一个或多个任意轴的数组组成。张量通常由普通大写字体表示,例如 X, Y, Z
1 X = torch.arange(24 ).reshape(2 , 3 , 4 )
1 2 3 4 5 6 tensor([[[ 0, 1, 2, 3],
张量算法的基本性质
两个矩阵按元素的乘法称为哈达玛积(Hadamard),即逐元素积,用数学符号
⊙
表示,示例如下:
A ⊙ B = [ a 11 b 11 a 12 b 12 … a 1 n b 1 n a 21 b 21 a 22 b 22 … a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 … a m n b m n ] .
1 2 3 a = torch.arange(9 ).reshape(3 , 3 )print (a * b)
1 2 3 tensor([[ 0, 1, 4],
降维
符号
∑ i = 1 d x i
表示对张量中的所有元素进行求和,代码表示如下:
1 2 3 4 x = torch.arange(4 , dtype=torch.float32)sum ()
求和不一定是全部轴一起计算,也可以单独计算某个指定轴
1 2 3 A_sum_axis0 = A.sum (axis=0 )
除了求和外,也可以取平均值,同样也可以指定计算哪一轴。
1 2 3 4 5 A.mean(), A.sum () / A.numel()0 ), A.sum (axis=0 ) / A.shape[0 ]8. , 9. , 10. , 11. ]), tensor([ 8. , 9. , 10. , 11. ]))
正常情况下,求和或求平均都会降低张量的维度。但是也可以让其保持维度
1 sum_A = A.sum (axis=1 , keepdims=True )
1 2 3 4 5 tensor([[ 6.],
cumsum 函数可用来对张量的元素进行逐个累加求和
1 2 3 x = torch.tensor([1 , 2 , 3 , 4 ])print (torch.cumsum(x, dim=0 ))
点积
两个向量的点积为相同位置的元素相乘后求和,
x , y ∈ R d
,
x T y = ∑ i = 1 d x i y i
1 2 3 y = torch.ones(4 , dtype = torch.float32)
1 (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
对于向量
x ∈ R d
,权重
w ∈ R d
,x 中的元素根据 w 权重的加权和,可以表示为点积
x T w
当权重的元素非负,且所有元素的加总值为 1 时,即
∑ i = 1 d w i = 1
, 此时二者的点积相当于 x 基于权重的加权平均;
将两个向量进行规范化,取得单位长度后,二者的点积表示两个向量夹角的余弦。该余弦值与夹角的大小有关。
cos θ = A ∥ A ∥ ⋅ B ∥ B ∥
其中:
∥ A ∥
表示向量的长度 =
a 1 2 + a 2 2 + ⋯ + a n 2
当夹角
θ
为 0 时,余弦值为 1,两个向量的方向相同
当夹角
θ
为 90 度时,余弦值为 0,两个向量的方向相互垂直;
当夹角
θ
为 180 度时,余弦值为 -1,两个向量的方向相反;
− 1 < c o s θ < 1
,表示两个向量的夹角介于 0 到 180 之间;越是接近 1,则夹角越小;
矩阵-向量积
假设有矩阵
A ∈ R m × n
,向量
x ∈ R n
,矩阵 A 使用行向量表示如下:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ]
矩阵与向量相乘后如下:
A x = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] x = [ a 1 ⊤ x a 2 ⊤ x ⋮ a m ⊤ x ] = [ m 1 m 2 ⋮ m n ]
相当于在行的维度上进行点积.
1 2 A.shape, x.shape, torch.mv(A, x)
矩阵-矩阵乘法
矩阵-矩阵乘法是矩阵-向量积的进一步拓展,假设有两个矩阵
A ∈ R n × k
和
B ∈ R k × m
:
A = [ a 11 a 12 ⋯ a 1 k a 21 a 22 ⋯ a 2 k ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n k ] , B = [ b 11 b 12 ⋯ b 1 m b 21 b 22 ⋯ b 2 m ⋮ ⋮ ⋱ ⋮ b k 1 b k 2 ⋯ b k m ]
将它们转成列向量和行向量的表示法:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] , B = [ b 1 b 2 ⋯ b m ]
这样矩阵的乘法就变成了普通的点积形式了:
C = AB = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] [ b 1 b 2 ⋯ b m ] = [ a 1 ⊤ b 1 a 1 ⊤ b 2 ⋯ a 1 ⊤ b m a 2 ⊤ b 1 a 2 ⊤ b 2 ⋯ a 2 ⊤ b m ⋮ ⋮ ⋱ ⋮ a n ⊤ b 1 a n ⊤ b 2 ⋯ a n ⊤ b m ]
1 2 3 A = torch.arange(20 ).reshape(5 , 4 )4 , 3 , dtype=torch.long)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
范数
向量的范数(norm) 表示一个向量有多大。向量的范数有如下一些特性
随元素等比缩放,
f ( α x ) = | α | f ( x )
三角不等式,
f ( x + y ) ≤ f ( x ) + f ( y )
非负,
f ( x ) ≥ 0
向量的
L 2
范数即是常见的欧几里得距离:
L 2 = ∥ x ∥ 2 = ∑ i = 1 n x i 2
1 2 3 u = torch.tensor([3.0 , -4.0 ])
向量的
L 1
范数则为各元素的绝对值之和:
L 1 = ∥ x ∥ 1 = ∑ i = 1 n | x |
向量的
L p
范数表示如下:
∥ x ∥ p = ( ∑ i = 1 n | x i | p ) 1 / p
可见
L 1
和
L 2
范数是
L p
范数在 p = 1 和 p = 2 时的情况;
除了向量可以计算范数,矩阵也一样可以计算范数。例如矩阵 X 的 Frobenius 范数即是矩阵各元素平方和的平方根
∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2
1 2 torch.norm(torch.ones((4 , 9 )))
深度学习的很多问题,经常表现为寻找这些问题的最优目标解,例如最小化差异,最小化距离、最大化概率等等;这些目标经常可以使用范数来表示,例如
L 2
范数的一个特性就是用来衡量两个向量之间的距离。因此,很多问题在数学上可以转化成求向量之间的范数(向量刚好可以用来表示物体的属性集合);
微积分
导数和微分
当我们选择损失函数时,需要选择一个可微的函数。这样才方便计算,当参数变化一个微小的幅度时,损失值将变化多少幅度。这两个幅度的比值,就是梯度变化。
偏导数
对于多变量的函数,例如 f(x, y),只改变其中一个变量,其他变量保持不变,计算出来的导数,称为偏导数。可以理解为函数在某个维度上面的变化率(假设每个变量对应一个维度)。
梯度
对于一个 n 维向量 x = [x1, x2, x3, …, xn],函数 f(x) 对于 x 的梯度,可以表示为一个 n 维偏导数组成的向量
链式法则
假设有两个单变量函数:y = f(u) 和 u = g(x),根据求导链式法则,存在:
接下来是多变量的场景,假设可微分函数 y 有 [u1, u2, u3, …, un] 个变量,其中每个可微分函数 ui 也有 n 个变量 [x1 , x2 , x3 , …, xn ],根据链式法则,存在
链式法则可用于多变量的复合函数的求导。
自动微分
在构建模型时,深度学习的框架会自动创建一个计算图,以便跟踪数据的整个计算过程。这个计算图后续可以很方便的用来实现自动微分,快速实现求导。
概率
基本概率论
概率论公理
在既定的样本空间 S 中,事件 A 发生的概率,用 P(A) 来表示,它有以下一些特性:
概率不会是负数,因此 P(A) >= 0;
整个样本空间发生的概率之和为 1,即 P(S) = 1;
对于多个互斥事件,它们整体发生的概率等于单个事件发生的概率之和;
序列 (1, 1, 2, 2, 3, 3, …)枚举的可数集是 {1, 2, 3},即序列关注的是元素的顺序,并且允许重复;集合不关注顺序,且不允许重复
随机变量
对于离散事件,比如骰子能投出 6 个面中的任意一个,每个面出现的概率为 1/6;但有些事件不是离散而是连续的,比如气温,身高。对于连续事件,如果无限精确计算的话,单个点的概率为 0, 这样在数学上就不好做计算了。因此,为方便计算,引入了概率密度。概率密度的计算可抽象成值落在某个区间的概率总和,除以区间的长度,或许可理解为一个单位长度的概率。
处理多个随机变量
联合概率
多个条件同时满足的概率,即 P(A = a, B = b),相当两个独立事件的交集。
显然,联合概率有以下特性:
P ( A = a , B = b ) ≤ P ( A = a )
注:P(A, B) 称为联合分布,联合分布有点像是各种组合的联合概率的总清单(目录),有点类似下面这个样子:
条件概率
条件概率是一个比率,示例如下:
0 ≤ P ( A = a , B = b ) P ( A = a ) ≤ 1
可简化表示为:
P ( B = b ∣ A = a )
可理解为:在 A = a 已经发生的情况下,出现 B = b 的概率;
贝叶斯定理
根据乘法法则,存在:
P ( A , B ) = P ( B ∣ A ) P ( A ) = P ( A ∣ B ) P ( B )
由以上等式,可换算:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B )
贝叶斯定理的核心思路是:随着新证据的出现,不断更新我们的看法(数学上表示为不断调整概率);
贝叶斯定理是为了解决逆向概率的计算问题。它有点像似然概率的计算,根据观察到的结果,倒推其正向概率。示例如下:
假设有 5 个白球,5 个黑球。那么从这 10 个球中,随机摸出一个白球的概率是 50%;这是正向概率计算。
逆向概率是指,我们不知箱子里面有几个白球和几个黑球。但我们可以先摸几把,然后猜测里面的白球和黑球的比例情况,以及各种情况的可能性大小。
结合垃圾邮件过滤的例子,来理解贝叶斯定理,其中:
P(A) 表示基于历史经验或统计,每 1000 封邮件中,会出现多少封邮件是垃圾邮件;
P(B) 表示当满足某个具体条件,例如邮件中包括“免费”两个字时,该封邮件有可能是垃圾邮件的平均概率,同样也是基于历史统计;
P(B | A) 表示每 100 封垃圾邮件中,有多少封邮件会包含“免费”两个字;
根据上面三个值,就可以计算出,当邮件中出现“免费”两个字时,有多大的概率,该封邮件是一份垃圾邮件。
假设:
P(A | B) 表示后验概率,即当 B 发生时,A 出现的概率是多少;
P(A) 表示先验概率,即根据过往经验, A 出现的概率是多少;
P(B | A) 表示似然概率,即当 A 发生时,B 出现的概率是多少;
因此,存在以下规律:后验概率 ∝ 先验概率 × 似然概率
∝ 表示正比于的关系。似然概率这个翻译很有意思,英文是 likelihood,直译应为可能性。其实意思上也正是如此,即表达可能性的大小。如果可能性很高,那么后验概率就会变大。如果可能性很低,那么后验概率相对先验证概率就会变小。因此,似然概率就可以理解为加强或者弱化先验概率的引擎,有可能增加马力,也有可能减少马力。
边际化
如果已知当 B 发生时,出现 A 的所有概率,那么加总这些概率(联合概率),就可以得到 B 发生的概率;
P ( B ) = ∑ A P ( A , B )
独立性
如果 A 的发生,与 B 是否发生无关,那么我们可以说这两个事件是相互独立的,在统计学中表示为
A ⊥ B
相当于 P(B | A) = P(B),P(A | B) = P(A)
存在:P(A, B) = P(A) * P(B)
期望和方差
期望值:一个随机变量,进行大量的重复实验,最后统计出来的平均值;可简单理解为理论上的平均值;例如抛硬币,假设正面得 1 分,反而得 0 分,那么抛了 10000 次后,理论上最后的平均得分是 0.5。
计算方法:每个可能的结果,乘以该结果发生的概率,表示如下:
E [ X ] = ∑ x x P ( X = x )
对于函数 f(x),如果 x 的概率分布为 P,那么 f(x) 的期望值为:
E x ∼ P [ f ( x ) ] = ∑ x f ( x ) P ( x )
方差
随机变量和平均值的差异,可使用方差量化:
Var [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − E [ X ] 2
差的平方的期望,等于平方的期望 - 期望的平方;以上公式借助期望的线性性,是可以推导的;
方差的平方根称为标准差。随机变量函数的方差用来衡量:当从样本空间中任意采样一个随机变量,它的值与平均期望值的偏离程度。
Var [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ]
线性性
对于任意的两个随机变量 X 和 Y,以及任意两个常数 a 和 b:
E [ a X + b Y ] = a E [ X ] + b E [ Y ]
不管两个变量之间是否存在依赖关系,以上公式都成立;期望的和等于和的期望;
或者任意数量的随机变量也可以:
E [ ∑ i = 1 n a i X i ] = ∑ i = 1 n a i E [ X i ]
常数的期望是常数自己,即:
E [ c ] = c
范数
范数:它是一个函数,这个函数可以将一个向量,映射到一个正数或0,这样就可以对这个向量做一些判断,如果知道的它长度、大小等属性;最常见的范数是求一个向量的欧几里得距离(长度);
范数需要满足三个特性:
非负,即映射后的结果需要 >= 0;
齐次: ||αx || = |α| · ||x ||
三角不等式:||x + y || ≤ ||x || + ||y ||
常见的向量范数
L~p~ 范数
其中参数 p >= 1,表示式如下:
L1 范数:当 p = 1 时,也称为曼哈顿范数
向量的所有分量的绝对值之和,在机器学习中可用于 L1 正则化。它的思路是将权重值汇总,乘以一个惩罚系数后,加到损失函数的结果中。
假设原损失函数为:Loss_original = Σ(y_i - ŷ_i)²
加入 L1 正则化后:Loss_Lasso = Loss_original + λ * Σ|w_j|
其中:
Σ|w_j|w_j 的绝对值之和;λ 是惩罚系数;0 表示不惩罚,越大则惩罚越重。如果惩罚很大,表示损失很大,会导致模型减少该权重值,甚至变成 0
正则化相当于不断逼迫模型使用尽量小的权重值,甚至将一些权重值设为 0,这样可以让模型变简单,防止过拟合。但是代价是过于激进的话,有可能导致模型变得欠拟合。
L1 正则化是绝对值之和,L2 正则化则取权重的平方和,它会让权重变小一些,但不至于变成 0,有助于仍然保留所有特征。
不管是 L1 还是 L2 正则化,它们的目标都是帮忙最小化损失函数。因为 L2 正则化使用的是平方和(二阶),因此它的导数(一阶)刚好跟权重大小成正比关系;这意味着它对权重的影响力,是动态的,权重值越大,它的影响力越大;权重值越小,它的影响力越小。有点像是一个弹簧,距离拉得很开的时候,弹簧受力越大。因此,当权重值接近 0 的时候,它的值因为平方的关系,会变得可以忽略不计。所以权重值不会完全变成 0;
L1 是绝对值之和,所以它的导数是一个常数,因此,它对权重的影响力是恒定的。所以随之迭代次数变多,它会不断将权重往 0 的方向推进,直到它变成 0;因此它可以用来实现稀疏性,剔除一些不重要的特征;
L2 范数,也称为欧几里得范数,用来计算欧几里得空间中,两点之间的直线距离。
它的使用场景包括:
线性神经网络
线性回归
线性回归:一种为自变量和因变量之间的关系进行建模的方法(可用来表示输入和输出之间的关系);
使用场景:当我们想要预测一个数值时,通常可使用线性回归;例如预测房屋价格、预测销量等;
背后思想:假设自变量和因变量之间的关系是线性的,即目标值等于特征值的加权和
基本元素
线性模型
示例:房屋价格 = 权重w1 × 面积 + 房龄 × 权重w2 + 偏置值 b
price = w area ⋅ area + w age ⋅ age + b
引入偏置项能够增加模型的表达能力。以上公式相当于对特征使用权重值进行仿射变换,然后使用偏置值进行平移;
之所以要仿射变换,是因为特征值只是我们人类在生活中自定义的一种标准,它并不一定是事物在数学中的标准,因此需要对其进行变换。
以上公式抽象后可表达如下:
y ^ = w 1 x 1 + . . . + w d x d + b
其中字母 y 的上边加个小尖,表示它是一个估计值;
引入矩阵后,以上公式可以进一步简化表示为:
y ^ = w ⊤ x + b
相当于将所有的权重 w 用向量 W 来表示,所有的特征用向量 x 来表示;
以上是单个样本的表示方法,对于所有样本,我们引入二维矩阵 X,每一行是一个样本,每一列一种属性
y ^ = X w + b
由于现实生活中房屋的价格组成是复杂的,并不仅仅由于面积和房龄两个因素确定。因此对于在模型的计算过程中,不可避免会存在少量误差(噪声);
损失函数
损失函数:用来量化预测值和实际值之间的误差大小;
线性回归问题中最常用的损失函数是计算平方差,即误差的平方
l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2
使用平方差有个好处是结果不会是负值,让计算更变得更简单了;
累加所有元素的预测损失,并计算其平均值:
L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2
模型训练的目标,是找到一组参数(w, b),让总体的损失平均值最小;
w ∗ , b ∗ = argmin w , b L ( w , b )
解析解
解析解:能够用数学公式精确表示的解,例如可以用初始函数(多项式、指数函数、对数函数、三解函数)+ 数学常数进行组合表达出来的解。
解析解的特点:
完全精确,没有误差,没有近似;
可用公式来表达所有的解,只要输入参数,就可以获得任意参数的解;
通用:只要符合适用条件,对于任意参数,都可以用该公式来求解;
线性回归问题由于足够简单,因此刚好能够求得解析解。
与解析解相对的是数值解,数值解的特点:
无法使用公式进行表达,而是近似解。
通常是一组具体的数字
解析解是数学上的完美答案,数值解是工程经验的总结;在现实世界中,当问题比较复杂时,由于影响因素太多,常常只能找到近似解。
梯度下降
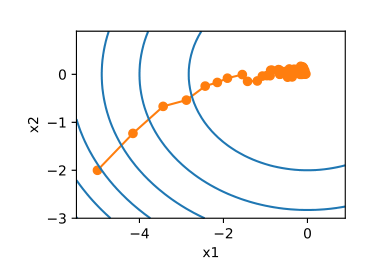
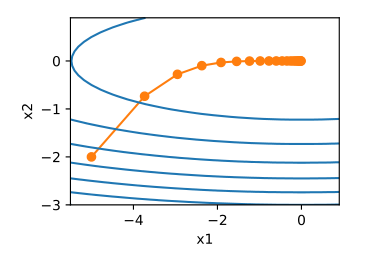
解析解意味着存在一个标准答案,没有误差。但很多时候,解析解是不存在的。尽管如此,我们仍然可以训练和优化模型参数。一种常用的方法是梯度下降,它的原理很简单,就是在让损失函数递减的方向上,不断调整参数值,最小化误差。
梯度即导数,它类似于变化速度。越陡的梯子,单位距离的变化率越大。越平缓的梯子,单位距离的变化率越小。
当数据集很大时,如果计算所有样本的导数,则计算量很大。一种解决方法是使用一个小批量的样本,来做近似计算得到梯度值。之后将梯度值乘以预告设定的一个正确(学习率),并从当前参数值中扣除,得到一个更新后的参数。相当于往下坡的方向,前进一点点。
批量大小和学习率是预先设定好的,在模型的训练过程中保持不变。批量大的话,有更大的代表性,因此学习率也可以考虑设置大一些,这样学习起来更快。如果指小,那学习率只能设置小一些,不然步子迈得太快,极左极右,反而学习起来变慢了(也即向正确值的收敛慢)。
当训练的数据量比较大时,需要一定数量的迭代次数,以便让参数调整到最佳状态;
矢量化加速
矢量化有助于实现并行计算,避免使用低效且成本高昂的 for 循环。
正态分布与平方损失
概率:已知原因,推导结果的可能性。
示例:已知硬币是均匀的,有一半的机会出抛出正面。有一半的机会抛出反面,即 e = 0.5。那么连续抛5次,其中有 3 次正面的概率有多大?
似然:已知结果,推导原因的可能性。
示例:已知抛了 5 次硬币,其中有 3 次正面,2 次反面。那么硬币是均匀的(e = 0.5)可能性有多大?或者说 e 为多少值时,最有可能抛出这种结果?
似然函数,就是根据结果,推算可能性
e
的一个函数;它可以用来表示,在给定的观测数据下,不同参数值的似然度。
当误差服从正态分布时,普通最小二乘法等价于最大似然估计。线性回归的目标,就是寻找让观测数据点出现的概率最大的回归线。
普通最小二乘法:对于一组数据点,找到一条直线,让各个数据点,到直线垂直距离的平方和最小。
从线性回归到深度网络
线性回归可以视只有一层的神经网络(即层数为 1);
线性回归-从零开始实现
生成数据集
1 2 3 4 5 6 7 8 9 10 11 12 13 """生成y=Xw+b+噪声""" def synthetic_data (w, b, num_examples ):0 , 1 , (num_examples, len (w)))0 , 0.01 , y.shape) return X, y.reshape((-1 , 1 ))2 , -3.4 ])4.2 1000 )
1 2 3 4 5 6 7 8 9 10 def data_iter (batch_size, features, labels ):len (features)list (range (num_examples))for i in range (0 , num_examples, batch_size):min (i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]
初始化待训练的权重参数 w 和偏置 b,
1 2 w = torch.normal(0 , 0.01 , size=(2 ,1 ), requires_grad=True )1 , requires_grad=True )
训练过程就是不断迭代更新这两个参数,让它们和数据集尽可能好的拟合数据集,让损失最小。
1 2 3 """线性回归模型""" def linreg (X, w, b ): return torch.matmul(X, w) + b
定义损失函数
1 2 3 """均方损失""" def squared_loss (y_hat, y ):return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
定义优化算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 """ 小批量随机梯度下降 Small-Batch SGD, Stochastic Gradient Descent 三个参数分别如下: params:参数的集合 lr:学习率 batch_size:批量大小 """ def sgd (params, lr, batch_size ):with torch.no_grad():for param in params:
经检查发现,此处的梯度计算真的是算总和,如下:
梯 度 梯 度 g ← ∂ ( w , b ) 1 | B | ∑ i ∈ B l ( x ( i ) , y ( i ) , w , b )
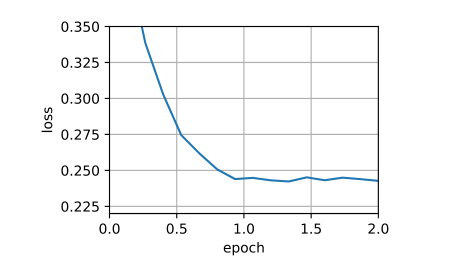
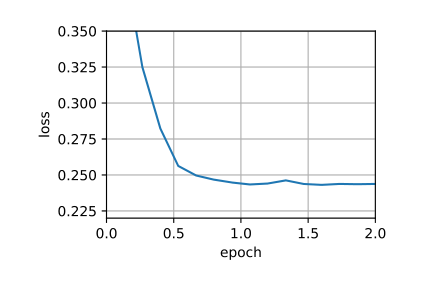
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 lr = 0.03 3 for epoch in range (num_epochs):for X, y in data_iter(batch_size, features, labels):sum ().backward() with torch.no_grad():print (f'epoch {epoch + 1 } , loss {float (train_l.mean()):f} ' )
注:backward 方法会计算当前张量相对于叶子节点的梯度,然后将结果存放在参数的 .grad 属性中
1 2 3 4 5 6 7 8 9 10 import torch2.0 , requires_grad=True )2 print (x.grad)
幂函数的求导法则:
d d x ( x n ) = n x n − 1
1 2 3 4 5 6 7 8 9 10 11 12 13 1.0 , 2.0 ], requires_grad=True ) 2 """ 此处 x 和 y 都是一个向量,因此需要提供梯度参数(权重),例如 torch.tensor([0.1, 0.2]), 此处的梯度参数 torch.tensor([0.1, 0.2] 代表的是上游梯度,形状必须跟 y 相同,以便从中取出对应索引位置的标量 """ 0.1 , 0.2 ]))print (x.grad) """ 之所以调用 y.backward 方法,会导致 x.grad 出现变化,是因为在使用 torch.tensor 初始化 x 时,设置了参数 requires_grad=True,因此 PyTorch 会自动创建计算图,记录 x 的计算过程,从而在计算中,能够找到 x 和 y 的关联; 另外,貌似 requires_grad=True 会传导,即计算出来的张量结果,也会自动默认为 requires_grad=True,这个传导性是 PyTorch 实现自动微分的关键; """
梯度计算必须是标量,如果是向量(由多个标量组成),说明这个向量只是中间结果,并不是最终结果。因此需要指明需要计算其中哪个标量的梯度(偏导数),或者指明如何组合这多个标量(求平均或者求和);
假设:
y = f ( x )
L = g ( y )
如果我们想要计算 L 对 x 的导数,也即
d L d x
,那么基于链式法则:
d L d x = d L d y ⋅ d y d x
其中:
d L d x
就是需要传入backward 方法的梯度权重参数;
或许可以这么理解,backward 方法是从标量开始的,如果不是标量,而是向量,那就需要告知之前的梯度是什么样子的。而且这个梯度参数是有要求的,它的形状必须与当前调用 backward 方法的张量的形状一致;
线性回归-简洁实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import numpy as npimport torchfrom torch.utils import datafrom d2l import torch as d2l2 , -3.4 ])4.2 1000 )def load_array (data_arrays, batch_size, is_train=True ): """构造一个PyTorch数据迭代器""" return data.DataLoader(dataset, batch_size, shuffle=is_train)10
全连接层:每一个输入,经过矩阵乘法后,都指向了一个输出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 from torch import nn2 , 1 )) 0 ].weight.data.normal_(0 , 0.01 )0 ].bias.data.fill_(0 )0.03 )3 for epoch in range (num_epochs):for X, y in data_iter:print (f'epoch {epoch + 1 } , loss {1 :f} ' )
在 PyTorch 中,每执行一次反向传播,其计算的梯度会累加到参数的 grad 数据上。可调用 zero_grad 方法清空之前的梯度值,这样就不会累积了
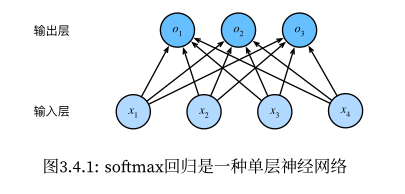
softmax 回归
线性回归用于预测值,softmax 回归则常用于预测分类。
分类的标签可使用多种数据结果来表示,例如直觉上可以用 1, 2, 3 来表示三个不同的类别。但是也可以使用向量来表示,例如 [1, 0, 0] 表示 1, [0, 1, 0] 表示 2, [0, 0, 1] 表示 3,这种方法称为“独热编码" one-hot encoding;
假设有 3 个类型,4 个特征,那么我们需要有一个仿射函数,用于将 4 个特征映射到 3 个类型上,示例如下:
o 1 = x 1 w 11 + x 2 w 12 + x 3 w 13 + x 4 w 14 + b 1 , o 2 = x 1 w 21 + x 2 w 22 + x 3 w 23 + x 4 w 24 + b 2 , o 3 = x 1 w 31 + x 2 w 32 + x 3 w 33 + x 4 w 34 + b 3 .
softmax 运算
在全连接层的仿射变换后,其结果有可能是负数、正数或零,而且所有结果加总后的值不一定是 1。显然,这个结果未规范化,不适合直接用来做概率。但我们可以使用指数函数(求幂)计算 + 规范化,将它们转成概率;
其 中 y ^ = softmax ( o ) 其中 y ^ j = exp ( o j ) ∑ k exp ( o k )
y ^
是一个概率分布;
exp(x) 表示求自然数 e 的 x 次方,即以自然数为底的指数函数;它可以用来描述一些连续增长或衰减的过程;且计算结果 >= 0;
softmax 回归的向量(矢量)计算表达式:
O = X W + b , Y ^ = softmax ( O ) .
损失函数
MLE:最大似然估计(Most Likelihood Estimation)
假设模型的参数为 θ ,我们希望找到一个最优的 θ 值,它使条件概率 P(Y | X) 得到最大值;
θ ^ MLE = arg max θ P ( Y ∣ X ; θ )
由于 X 和 Y 是独立变量的集合,因此条件概率 P(Y | X) 是每一个独立变量的条件概率的乘积:
P ( Y ∣ X ) = ∏ i = 1 n P ( y ( i ) ∣ x ( i ) )
乘积有两个问题:
概率的值区间为 [0, 1],多个概率相乘,其结果会越来越小。由于存储的位数是有限,有可能会造成溢出(下溢);
乘积的方式也不方便求导数;
为了解决以上问题,我们给以上表达式取对数,因为乘积的形式,在取完对数后,变成了求和;示例如下:
log P ( Y ∣ X ; θ ) = log ( ∏ i = 1 n P ( y ( i ) ∣ x ( i ) ; θ ) ) = ∑ i = 1 n log P ( y ( i ) ∣ x ( i ) ; θ )
此处我们相当于转换了问题的形式,将求最大化原始似然概率的问题,转换了求最大化对数似然概率的问题;
arg max θ P ( Y ∣ X ; θ ) = arg max θ ∑ i = 1 n log P ( y ( i ) ∣ x ( i ) ; θ )
注意:由于概率 0 <= P <= 1,因此对概率取对数的话,得到的结果是负数;
参数优化的目标,是让损失越来越小,也就是让损失函数的值最小化。因此,我们还需要进一步转化问题,将”最大化对数似然“,转变一个最小化的问题。此时有一个简单的办法,就是将求负数的最大值(因为 logP 的结果是负数),变成求正数的最小值(负对数似然 NLL Negative Log Likelihood),示例如下:
NLL ( θ ) = − log P ( Y ∣ X ; θ ) = − ∑ i = 1 n log P ( y ( i ) ∣ x ( i ) ; θ )
因此:
arg max θ log P ( Y ∣ X ; θ ) = arg min θ ( − log P ( Y ∣ X ; θ ) )
解析如下:
*
P ( y ( i ) ∣ x ( i ) ; θ )
越大,说明预测的准确率越高;
log P ( y ( i ) ∣ x ( i ) ; θ )
的结果是负数,因为 P < 1;值越大,则越接近 0;
− log P ( y ( i ) ∣ x ( i ) ; θ )
的结果是正数,越小越好,即越接近 0;
经过以上三步,将一个求最大值的问题,变成了一个求最小值的问题。负对数似然相当于一种损失函数,预测的概率越高,该损失函数的结果就越小。反之,预测的概率越低,损失越大;该损失函数(交叉熵)表示如下:
l ( y , y ^ ) = − ∑ j = 1 q y j log y ^ j
y j
是一个独热向量,这意味着其中只有某个维度上有值;
log y ^ j
是负数,
− log y ^ j
则好变成正数;
熵是信息论中的一个概率,它可用来度量一个系统的不确定性程度。熵越大,表示不确定性越大,系统越混乱。模型预测的概率,通常不能和真实概率一模一样,二者存在一定的差异。因此,我们引入熵的概率,来衡量差异的大小。熵越大,表示差异越大,预测的越不准。
交叉熵中的”交叉“一词,原因在于我们用真实概率分布与预测概率分布进行交叉(匹配)计算, 即公式中
y j
和
log y j ^
的配对。熵原本只是用来衡量某个概率分布内部的不确定性。但在计算损失时,我们将两个概率分布进行交叉匹配,以计算每个分项的不确定性。
二元交叉熵损失函数的公式为:
Loss = − [ y log ( y ^ ) + ( 1 − y ) log ( 1 − y ^ ) ]
由于 y 是独热编码,所以 y 的值要么为 0,要么为 1
当 y = 1 时,公式变成了:
Loss = − log ( y ^ )
当 y = 0 时,公式变成了:
Loss = − log ( 1 − y ^ )
softmax 及其导数
y ^ j = exp ( o j ) ∑ k exp ( o k )
l ( y , y ^ ) = − ∑ j = 1 q y j log y ^ j
l ( y , y ^ ) = − ∑ j = 1 q y j log exp ( o j ) ∑ k = 1 q exp ( o k ) = ∑ j = 1 q y j ( log ∑ k = 1 q exp ( o k ) − log exp ( o j ) ) = ∑ j = 1 q y j ( log ∑ k = 1 q exp ( o k ) − o j ) = ∑ j = 1 q y j log ∑ k = 1 q exp ( o k ) − ∑ j = 1 q y j o j = log ∑ k = 1 q exp ( o k ) − ∑ j = 1 q y j o j .
注:此处用到了对数的性质,即
log A B = log A − log B
以及
∑ j = 1 q y j = 1
的特点(独热向量)
对任一未规范化的结果
o j
进行求导:
∂ o j l ( y , y ^ ) = exp ( o j ) ∑ k = 1 q exp ( o k ) − y j = softmax ( o ) j − y j = y ^ − y j
求导结果非常简单,就是两个概率分布直接相减,即可得到梯度;之后可将此梯度传给前一层,实现反向传播;
信息论基础
熵
英文 entropy,对于概率分布 P,它的熵的计算公式如下:
H [ P ] = ∑ j − P ( j ) log P ( j )
信息量
香农使用
log 1 P ( j )
=
− log P ( j )
表示信息量,它有点类似我们在收到信息后的惊讶程度;如果信息量很大,我们就会很惊讶。如果信息量很小,我们则不怎么惊讶。当概率 P 越大时,
− log P ( j )
的值就越小。这意味着对于确定性很高的事件,我们不会感到太惊讶。但如果概率 P 很小,当它发生时,我们就会感到很惊讶,此时
− log P ( j )
的值很大。
重新看待交叉熵
交叉熵可以理解为:已知主观概率为 Q 的观察者,在看到基于概率 P 生成的数据时,感到的惊讶程度;当 P = Q 时,惊讶程度最小。
模型评估
预测 100 次,正确预测的次数为 60 次,那么正确比率为 0.6,该比率可用来评测一个模型的预测能力。正确比率越高,模型越好。
softmax 从零开始实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 import torchfrom IPython import displayfrom d2l import torch as d2l256 784 10 0 , 0.01 , size=(num_inputs, num_outputs), requires_grad=True )True )def softmax (X ):sum (1 , keepdim=True )return X_exp / partitiondef net (X ):1 , W.shape[0 ]))return softmax(torch.matmul(X_reshape, W) + b)def cross_entropy (y_hat, y ):return - torch.log(y_hat[range (len (y_hat)), y])""" y_hat[range(len(y_hat)), y] 是一个非常有意思的 Numpy 操作 它表示将 y 的值作为列,从 y_hat 每一行中,取出相应列的值 假设 y_hat 的 值为: y_hat = [[0.1, 0.3, 0.6], # 样本0:预测类别2的概率是 0.6 [0.8, 0.1, 0.1], # 样本1:预测类别0的概率是 0.8 [0.2, 0.7, 0.1]] # 样本2:预测类别1的概率是 0.7 y = [2, 0, 1] 目标:从 y_hat 每一行中分别取第2列、第0列、第1列的值,range(3) 用来表示要取值的行 # y_hat[range(3), y] → [y_hat[0,2], y_hat[1,0], y_hat[2,1]] → [0.6, 0.8, 0.7] """ def accuracy (y_hat, y ):if len (y_hat.shape) > 1 and y_hat.shape[1 ] > 1 :1 )type (y.dtype) == yreturn float (cmp.type (y.dtype).sum ())def evaluate_accuracy (net, data_iter ):if isinstance (net, torch.nn.Module):eval () 2 )with torch.no_grad():for X, y in data_iter:return metric[0 ] / metric[1 ]class Accumulator :def __init__ (self, n ):self .data = [0.0 ] * ndef add (self, *args ):self .data = [a + float (b) for a, b in zip (self .data, args)]def reset (self ):self .data = [0.0 ] * len (self .data)def __getitem__ (self, idx ):return self .data[idx]def train_epoch_ch3 (net, train_iter, loss, updater ):if isinstance (net, torch.nn.Module):3 )for X, y in train_iter:if isinstance (updater, torch.optim.Optimizer):else :sum ().backward() 0 ])float (l.sum ()), accuracy(y_hat, y), y.numel())return metric[0 ] / metric[2 ], metric[1 ] / metric[2 ]""" PyTorch 会自动创建一个计算图,以张量为节点,以操作为边。在模型进行前向传播计算时,框架会自动记录所有涉及张量以及相关操作到计算图中;当调用损失 loss.backward 方法时,会自动触发计算图的反向遍历,根据链式法则,计算参与前向传播计算的张量的梯度; 损失 loss 必须是标量,如果不是,则需要调用 sum 或者 mean 方法进行聚合,以便转成标量; 当使用 PyTorch 的 torch.tensor 方法初始化张量时,如果参数 requires_grad=True,那么它就会自动构建计算图。通过调用 torch.no_grad 方法,可以临时关闭计算图构建功能。 不可微分的操作,例如 argmax 离散操作,会中断梯度链。 """ """ updater.zero_grad() # 清零历史梯度 l.mean().backward() # 反向传播,计算梯度(取平均值) updater.step() # 更新参数 以上这三个操作很有意思,咋一看,backword 和 updater.step 之间并没有参数传递,好像没有什么关系 为什么能够实现参数的更新呢? 原因在于 loss 是计算结果,PyTorch 在背后悄悄维护着计算图,PyTorch 知道这个 loss 是如何一步一步计算出来的。 因此,当调用 backward 时,PyTorch 沿着计算图,计算出每一步的梯度变化,并将变化值存放在每一步涉及的张量的 grad 属性中。因为权重参数是参与计算的,所以权重参数在 backword 之后,其 grad 属性就被悄悄的赋值了; 而之前 updater 在初始化时,就已经将权重做为参数传进去了,所以 updater 里面关联着待更新的权重参数 当调用 step 方法时,updater 只需执行一下 param = param - lr * param.grad 即可; """ def train_ch3 (net, train_iter, test_iter, loss, num_epochs, updater ):'epoch' , xlim=[1 , num_epochs], ylim=[0.3 , 0.9 ]'train_loss' , 'train_acc' , 'test_acc' ])for epoch in range (num_epochs):1 , train_metrics + (test_acc,))assert train_loss < 0.5 , train_lossassert train_acc <= 1 and train_acc > 0.7 , train_accassert test_acc <= 1 and test_acc > 0.7 , test_acc0.1 def updater (batch_size ):return d2l.sgd([W, b], lr, batch_size)10 def predict_ch3 (net, test_iter, n=6 ):for X, y in test_iter:break 1 ))'\n' + pred for true, pred in zip (trues, preds)]0 :n].reshape((n, 28 , 28 )), 1 , n, titles=titles[0 :n])
softmax 简洁实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchfrom torch import nnfrom d2l import torch as d2l256 784 , 10 ))def init_weights (m ):if type (m) == nn.Linear:0.01 )
使用 softmax 函数直接计算概率的话,如果某个参数 x 的值很大,那么 exp(x) 很可能会导致溢出。为避免这个问题,可以先找到最大 x,然后所有值减去该最大值。这样得出来的都是负的,最大值是 0;
y ^ j = exp ( o j − max ( o k ) ) exp ( max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) exp ( max ( o k ) ) = exp ( o j − max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) .
由于后续计算交叉熵时,会取对数,因此,可以进一步计算如下:
log ( y ^ j ) = log ( exp ( o j − max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) ) = log ( exp ( o j − max ( o k ) ) ) − log ( ∑ k exp ( o k − max ( o k ) ) ) = o j − max ( o k ) − log ( ∑ k exp ( o k − max ( o k ) ) ) .
此处的做法即 LogSumExp 技巧,一种用来实现稳定计算的办法;
LSE ( x ) = c + log ( ∑ i = 1 n exp ( x i − c ) )
注:c 为
x i
的最大值,即
max ( x )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 'none' )0.1 )10
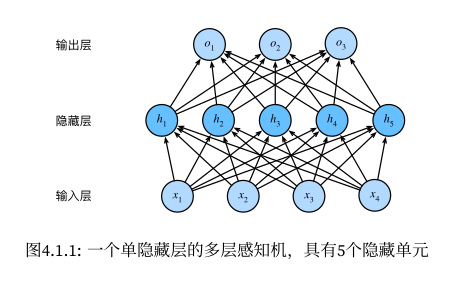
多层感知机
多层感知机
隐藏层
特征与目标有可能不是线性的关系,此时可考虑通过添加隐藏层(一个或多个)的方式,来处理特征和目标之间更复杂的关系。
由于输入层不涉及计算,因此以上模型的层数为 2 层;该多层感知机,有 4 个输入,3 个输出;
仿射变换是线性的,故无法处理非线性的关系。因此,可通过引入激活函数,来解决非线性关系的问题。
softmat 函数的计算单位是一行,激活函数的计算单元是一个元素,即逐个元素进行处理,而不是一整行的所有元素合并处理。
通过堆叠多个带激活函数的隐藏层,就能够构建出更具表达力的模型。事实上,只要有足够的神经元 + 权重参数,即使上单隐藏层的模型,也能够模拟所有的非线性函数。但这种处理方式是低效的。我们有可能通过增加隐藏层的层数,让问题更加高效的解决。
激活函数
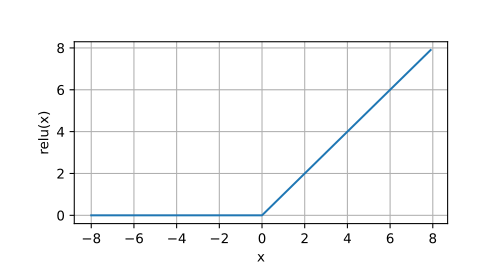
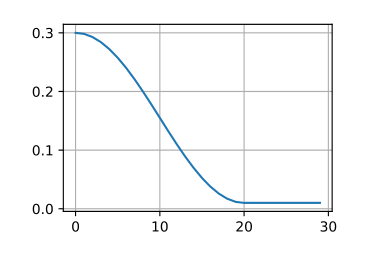
ReLU 函数
ReLU,Rectified linear unit,修正线性单元。
R e L U ( x ) = m a x ( x , 0 )
它的作用是保留正值,并将负数统统设为 0;调整后类似下面这个样子:
当输入为正数时,激活函数的导数为 1;当输入为负数或零时,其导数为 0;
ReLU 有很多变体,其中一种变体是增加一个线性项,以便在特定情况下,负数的参数也有效;
p R e L U ( x ) = m a x ( 0 , x ) + α ⋅ m i n ( 0 , x )
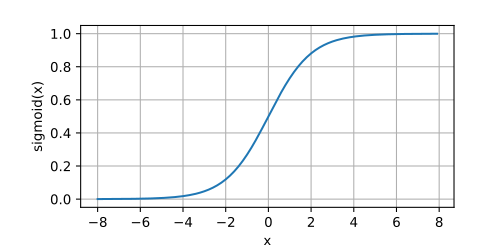
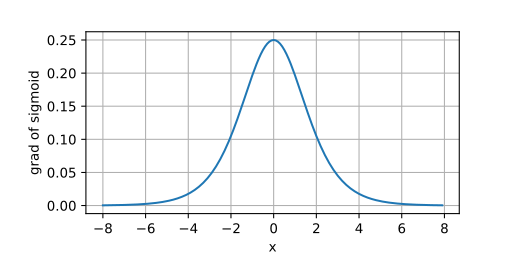
sigmoid 函数
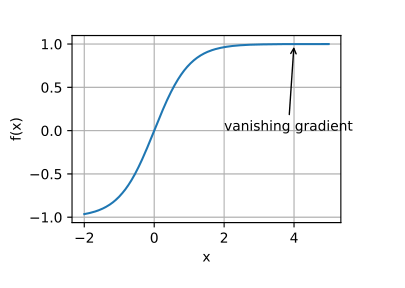
sigmoid 函数可将任意输入压缩到 (0, 1) 之间,所以也叫做挤压函数;
s i g m o i d ( x ) = 1 1 + exp ( − x )
其图像如下:
在二分类问题中,sigmoid 函数仍然广泛做在输出层中使用(可视为 softmax 函数的特例),但在隐藏层用得很少了,因为它有以下一些缺点:
容易造成梯度消失,因为导数的最大值为 0.25;当多个梯度连乘时,梯度值急剧缩小;这会导致头部层的权重无法有效更新,收敛慢,学习效率低;
值仅在 [-3, 3] 区域敏感;当
| x | > 5
时,梯度接近消失了;
输出的区间为 [0, 1],不是以零为中心,这会导致下一层的输入全部变成正的;权重更新容易出现剧烈的摆动,收敛速度慢;
指数运算的成本比较高;
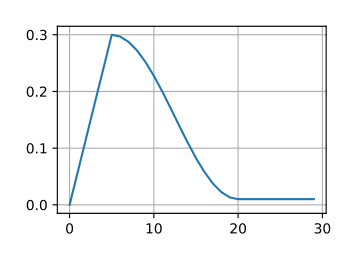
导数图像类似钟形曲线,示意如下:
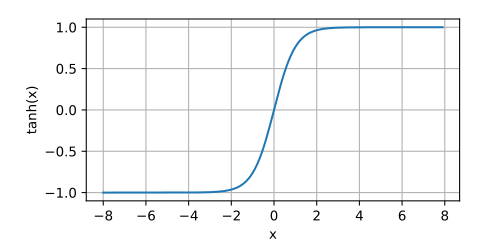
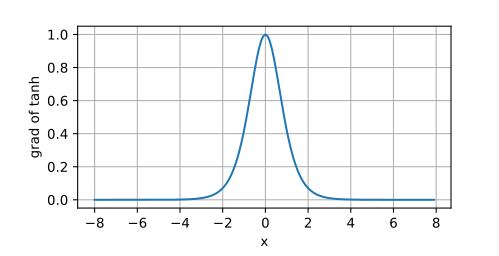
tanh 函数
tanh 函数可将任意输入值压缩到 [-1, 1] 区间,其转换公式如下:
t a n h ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x )
其导数图像如下:
由于 tanh 零点对称,而且导数最大值为 1, 因此它克服了 sigmoid 的一些缺点,例如梯度消失和摆动问题。但其敏感值区域仍然很小,大约在 [-2, 2] 之间;
多层感知机从零开始实现
1 2 3 4 5 6 import torchfrom torch import nnfrom d2l import torch as d2l256
初始化模型参数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 """ 此处输入为 784, 输出为 10, 隐藏单元的数量为 256(一般选择 2 的幂次,以便能够更高效的使用内存) """ 784 , 10 , 256 True ) * 0.01 )True ))True ) * 0.01 )True ))
激活函数
1 2 3 4 def relu (X ):return torch.max (X, a)
模型
1 2 3 4 5 def net (X ):1 ,num_inputs))return (H@W2 + b2)
损失函数
1 2 'none' )
训练
1 2 3 4 10 , 0.1
多层感知机的简洁实现
1 2 3 import torchfrom torch import nnfrom d2l import torch as d2l
模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 """ 之前的 softmax 模型是这样子的: net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) 现在相当于在中间加了两层,一层是 nn.Linear(784, 256), 一层是 nn.ReLU() """ 784 , 256 ),256 , 10 ))def init_weights (m ):if type (m) == nn.Linear:0.01 )
1 2 3 4 5 6 7 256 , 0.1 , 10 'none' )
以上示例的隐藏单元数量为 256;理论上隐藏单元越多,模型就能够拟合越复杂的函数。因此,如果数量太少,则模型无法存储足够多的参数,表达能力有限,出现欠拟合;如果太多,则模型容易和训练数据过拟合,泛化能力有限;
如果训练的数据集比较大,理论上应该用较多的隐藏单元来拟合。但同时可能需要考虑使用正则化技术来防止过拟合。正则化技术包括(dropout、L1/L2 正则化、早停等)
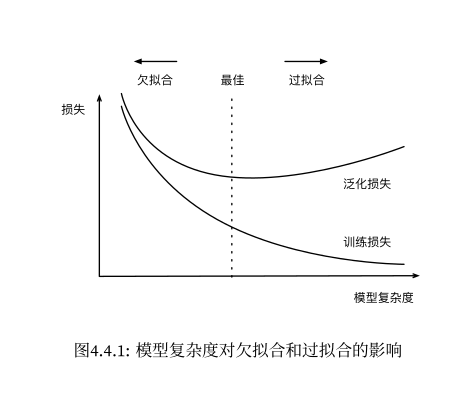
模型选择、欠拟合和过拟合
训练误差和泛化误差
当训练误差明显小于验证误差时,说明出现了过拟合。一些容易导致过拟合的因素包括:
参数的数量比较多;
参数的取值范围比较大;
训练样本的数量太少;
模型选择
模型选择涉及两个方面:
选择哪一类的模型,例如决策树还是多层感知机;
选择什么样的超参数;
如果样本数量太小,有一种勉强补救的办法是 K 折交叉验证。它的原理是将数据分成 K 份。每次在其中的 K - 1 份上训练,在剩下的1份中验证;循环一轮后,对实验结果取平均值;
欠拟合还是过拟合
如果没有足够的数据,有可能简单的模型效果更好。大多数深度学习模型,通常只有在拥有几千个样本的情况下,其表现才会比简单的线性模型更好。
多项式回归
多项式:由多个”项“相加组成的表达式;它涉及几个概念,以多项式
y = 3 x 2 − 2 x + 5
作为示例:
项:包括
3 x 2
,
− 2 x
,
5
等三个项;
系数:每个项中,乘以变量的常数,它们分别是: 3, -2
变量:表示能够取不同值的量,一般使用字母表示,此时是 x
次数
单项式:所有变量的指数之和
3 x 2
次数为 2
− 2 x y 3
次数为 1 + 3 = 4;
多项式:次数最高的项的次数;
3 x 2 − 2 x + 5
次数为 2(称为二次三项式)
常数项: 此处为 5
以下表达式不是多项式:
1/x 或 x⁻¹,因为指数为负数;
x
或者 x^(1/2),因为指数是分数;
2 x
,因为变量在指数位置,变成了指数函数;
sin(x),因为是三角函数
简单线性回归假设因变量 y 和自变量 x 之间是简单的线性关系。但有些场景中,它们俩可能是曲线关系,例如抛物线。此时需要引入 x 的高次项,用多项式构建模型。
y = β 0 + β 1 x + β 2 x 2 + β 3 x 3 + ⋯ + β n x n + ε
虽然自变量 x 是高阶的,但是系数
β
仍然是线性的,模型是这些系数的线性组合;
生成数据集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import mathimport numpy as npimport torchfrom torch import nnfrom d2l import torch as d2l20 100 , 100 0 :4 ] = np.array([5 , 1.2 , -3.4 , 5.6 ]) 1 ))1 , -1 ))for i in range (max_degree):1 ) 0.1 , size=labels.shape)
经过以上一顿折腾,实际上生成的多项式为:
y = 5 + 1.2 x − 3.4 x 2 2 ! + 5.6 x 3 3 ! + ϵ where ϵ ∼ N ( 0 , 0.1 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 for x in [true_w, features, poly_features, labels]]def evaluate_loss (net, data_iter, loss ): """评估给定数据集上模型的损失""" 2 ) for X, y in data_iter:sum (), l.numel())return metric[0 ] / metric[1 ]def train (train_features, test_features, train_labels, test_labels, num_epochs=400 ):'none' )1 ]1 , bias=False ))min (10 , train_labels.shape[0 ])1 ,1 )),1 ,1 )),False )0.01 )'epoch' , ylabel='loss' , yscale='log' ,1 , num_epochs], ylim=[1e-3 , 1e2 ],'train' , 'test' ])for epoch in range (num_epochs):if epoch == 0 or (epoch + 1 ) % 20 == 0 :1 , (evaluate_loss(net, train_iter, loss),print ('weight:' , net[0 ].weight.data.numpy())
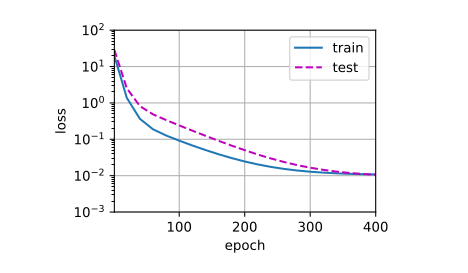
三阶多项式函数拟合
1 2 3 4 ], poly_features[n_train:, :4 ],
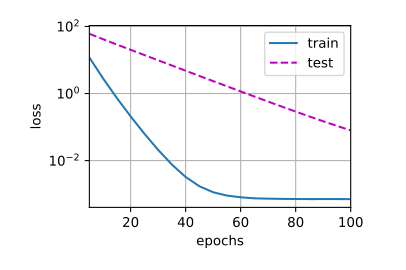
当使用三阶多项式的函数时,由于它和生成数据的函数阶段相同,因此,在训练过程中,能够有效的降低损失,学习到的系数值也和真实值接近
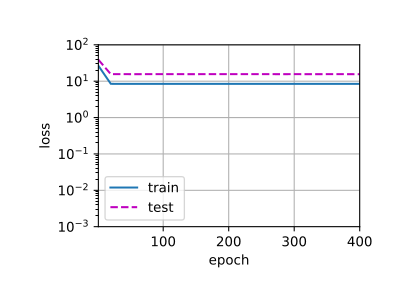
线性函数拟合
1 2 3 2 ], poly_features[n_train:, :2 ],
当使用线性函数拟合时,因为阶数不足,所以拟合效果不好,损失无法有效下降,处于欠拟合的状态
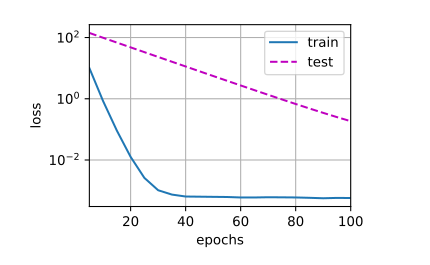
高阶多项式函数拟合
1 2 3 1500 )
当阶段过高时,如果训练的数据不足,其训练出来的系数很不稳定。表面上看训练损失快速降低,但验证损失仍然很高,说明出现了过拟合,未能很好的泛化。
判断是否使用多项式回归模型:
将数据可视化,绘制散点图,观察呈直线分布,还是曲线分布;
优先使用简单线性回归,如果不能拟合,再使用多项式回归;
权重衰减
截止目前,我们在优化权重参数时,并没有取值限制,它完全是根据梯度和学习率进行计算的。有时候权重参数会过大,相比其他权重参数出现了失衡,导致模型容易出现过拟合。因此,我们有必要引入一些机制(权重衰减技术),来引导权重的更新过程。其中一个方法是引入惩罚机制,也就是相同损失值的情况下,奖励小权重,惩罚大权重。逼迫模型尝试以更小的权重值,实现相同的损失。这样有助于避免拟合(某些权重参数过于喧宾夺主,形成虚假关联)。
L ( w , b ) + λ 2 ∥ w ∥ 2
λ (lambda)的大小决定了我们对权重约束的大小。如果 λ 很大,那么惩罚就会很大。
高维线性回归
1 2 3 import torchfrom torch import nnfrom d2l import torch as d2l
使用以下公式生成数据:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ where ϵ ∼ N ( 0 , 0.01 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 """ 样本数非常小,只有 20 个样本 输入的维数(特征数)非常多,有 200 个 """ 20 , 100 , 200 , 5 """ 合成数据的权重为 0.01,偏置为 0.05, 通常合成的时候还会添加噪声 公式示例:y = X @ true_w + true_b + noise """ 1 )) * 0.01 , 0.05 False )
从零开始实现
初始化模型参数
1 2 3 def init_params ():0 , 1 , size=(num_inputs, 1 ), requires_grad=True )1 , requires_grad=True )
定义 L2 范数用于惩罚
1 2 def l2_penalty (w ):return torch.sum (w.pow (2 )) / 2
定义训练代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def train (lambd ):lambda X: d2l.linreg(X, w, b), d2l.squared_loss100 , 0.003 'epochs' , ylabel='loss' , yscale='log' ,5 , num_epochs], legend=['train' , 'test' ])for epoch in range (num_epochs):for X, y in train_iter:sum .backward()if (epoch + 1 ) % 5 == 0 :1 , (d2l.evaluate_loss(net, train_iter, loss),print ('w 的 L2 范数是:' , torch.norm(w).item())
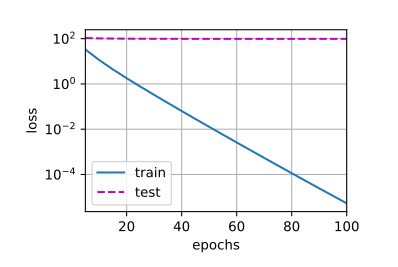
忽略正则化
1 w的L2范数是: 12.963241577148438
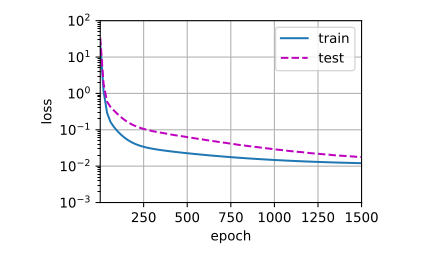
训练损失线性下降,但验证损失纹丝不动,模型严重过拟合
使用权重衰减
1 w的L2范数是: 0.3556520938873291
虽然验证损失与训练损失仍然有不少差距,但二者都开始收敛。之所以差距这么大,主要在于训练的样本数相对于特征数来说,实在太少了(样本只有 10 个,特征数量却有 200 个);
简洁实现
PyTorch 直接将权重衰减算法集成到了优化算法中,可在初始化优化算法中,通过 weight_decay 超参数传入想要使用的权重误差算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def train_concise (wd ):1 ))for param in net.parameters():'none' )100 , 0.003 "params" :net[0 ].weight,'weight_decay' : wd}, "params" :net[0 ].bias}], lr=lr)'epochs' , ylabel='loss' , yscale='log' ,5 , num_epochs], legend=['train' , 'test' ])for epoch in range (num_epochs):for X, y in train_iter:if (epoch + 1 ) % 5 == 0 :1 ,print ('w的L2范数:' , net[0 ].weight.norm().item())
1 w的L2范数: 0.3890590965747833
暂退法
一个模型的预测误差,存在三种情况:
偏差:描述预测值和实际值之前的差距。偏差大,说明模型不能很好的预测,性能不行,欠拟合;
方差:描述模型在不同的数据集上的训练结果波动很大,说明模型对不同的训练数据微小波动很敏感,出现过拟合;
不可约误差:一些未知因素引起的误差,例如训练数据本身有噪声,这类误差难以通过调整模型来消除;
重新审视过拟合
线性模型将每个输入特征视为独立的,深度模型则将它们视为关联的。对于那些并没有真正关联的特征,深度模型有可能会误入歧途,导致过拟合。
扰动的稳健性
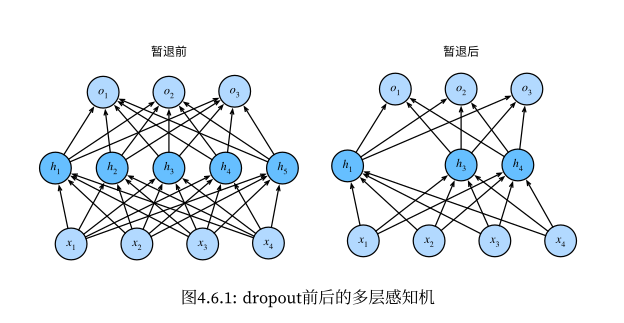
好的模型的一个标准是具备更强的鲁棒性,针对未曾见过的数据,模型的预测依然保持水准。为了提升鲁棒性,有一种技术是在模型的每一层中,引入 dropout,即故意丢弃一些计算结果(例如将其置0);这种丢弃动作有点类似在模拟噪声,让模型在有噪声的环境中进行训练,这样可提高的预测能力;因为模型不能完全依赖于任意一个节点(该节点有可能会被 dropout),从而避免模型产生过拟合。
假设 dropout 的概率为 p,则表达式为:
概 率 为 其 他 情 况 h ′ = { 0 概率为 p h 1 − p 其他情况 1 − p
之所以需要除以 h/(1 - p),是为了保持期望值不变,即
E [ h ′ ] = h
实践中的暂退法
dropout 一般仅在训练阶段使用,验证阶段则不启用。如果启用,一般可用于测试模型的预测稳定性。
从零开始实现
1 2 3 4 5 6 7 8 9 10 11 12 import torchfrom torch import nnfrom d2l import torch as d2ldef dropout_layer (X, dropout ):assert 0 <= dropout <= 1 if dropout == 1 :return torch.zeros_like(X)if dropout == 0 :return Xfloat ()return mask * X / (1.0 - dropout)
1 2 3 4 5 X = torch.arange(16 , dtype = torch.float32).reshape((2 , 8 ))print (X)print (dropout_layer(X, 0. ))print (dropout_layer(X, 0.5 ))print (dropout_layer(X, 1. ))
1 2 3 4 5 6 7 8 9 10 11 tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],# dropout = 0 # dropout = 0.5, 没有被丢弃的,新值 = 原值 / 0.5 # dropout = 1
定义模型参数
1 num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784 , 10 , 256 , 256
定义模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 dropout1, dropout2 = 0.2 , 0.5 class Net (nn.Module):def __init__ (self, num_inputs, num_outputs, num_hiddens1, num_hidden2, is_trainning=True ):super (Net, self ).__init__()self .num_inputs = num_inputsself .training = is_trainingself .lin1 = nn.Linear(num_inputs, num_hiddens1)self .lin2 = nn.Linear(num_hiddens1, num_hiddens2)self .lin3 = nn.Linear(num_hiddens2, num_outputs)self .relu = nn.ReLU()def forward (self, x ):self .relu(self .lin1(X.reshape((-1 , self .num_inputs))))if self .training == True :self .relu(self .lin2(H1))if self .training == True :self .lin3(H2)return out
训练和测试
1 2 3 4 5 6 10 , 0.5 , 256 'none' )
简洁实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 net = nn.Sequential(784 , 256 ),256 , 256 )256 , 10 ),def init_weights (m ):if type (m) == nn.Linear:0.01 )
前向传播、反向传播和计算图
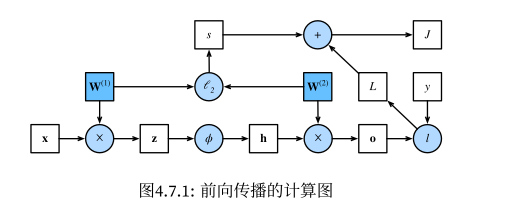
前向传播
假设输入样本为 x,经过第一层参数后得到 z
z = W ( 1 ) x
z 经过激活函数
ϕ
计算后得到 h
h = ϕ ( z )
h 经过输出层的参数计算后得到 o
o = W ( 2 ) h
假设损失函数为 loss,样本标签为 y,则单个样本的损失项为:
L = l o s s ( o , y )
假设正则化的超参数为
λ
, 则正则化项 s 为:
s = λ 2 ( ∥ W ( 1 ) ∥ F 2 + ∥ W ( 2 ) ∥ F 2 )
表达式中的字母 F 表示 Frobenius 范数,矩阵的 Frobenius 范数等于矩阵展平后,各元素的平方和的平方根。有点类似 L2 范围在矩阵上的一种应用。可用来衡量矩阵的“大小”;
正则化后的损失 J 为:
J = L + s
前向传播计算图
以上各步计算汇总后的计算图如下:
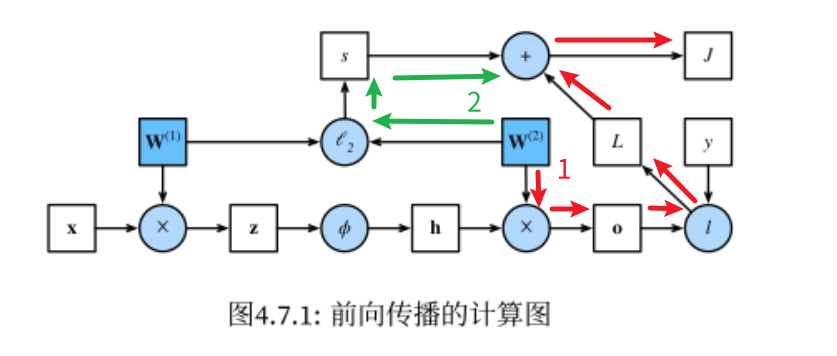
反向传播
对于最终的损失 J,反向传播的目的是计算它相对于权重参数的梯度,即
∂ J / ∂ W ( 1 )
和
) ∂ J / ∂ W ( 2 )
第一步:计算目标函数 J = L + s 关于 L 和 s 的梯度,因为是常数,所以梯度为 1
和 ∂ J ∂ L = 1 和 ∂ J ∂ s = 1
第二步:计算目标函数 J 关于最后一层的输入
o
的梯度:
∂ J ∂ o = p r o d ( ∂ J ∂ L , ∂ L ∂ o ) = ∂ L ∂ o
第三步:计算正则化项 s 关于权重参数的梯度:
和 ∂ s ∂ W ( 1 ) = λ W ( 1 ) 和 ∂ s ∂ W ( 2 ) = λ W ( 2 )
第四步:计算目标函数 J 关于最后一层权重参数
W ( 2 )
的梯度:
∂ J ∂ W ( 2 ) = prod ( ∂ J ∂ o , ∂ o ∂ W ( 2 ) ) + prod ( ∂ J ∂ s , ∂ s ∂ W ( 2 ) ) = ∂ J ∂ o h ⊤ + λ W ( 2 )
注:对于
o = W ( 2 ) h
, 其导数为
∂ o ∂ W ( 2 ) = h T
(不严谨的简写,并不是真正意义上的相等,而是在链式求导中可以替换),它想表达的核心意思是,在链式求导中,梯度的计算依赖于输入 h 的转置和输出误差的乘积;,也即:
∂ J ∂ W ( 2 ) = ∂ J ∂ o h ⊤
在计算图上面,从
W ( 2 )
到达目标函数 J 有两条路径:
第五步:计算目标函数 J 对于隐藏层 h 的梯度:
∂ J ∂ h = prod ( ∂ J ∂ o , ∂ o ∂ h ) = W ( 2 ) ⊤ ∂ J ∂ o
第六步:计算目标函数 J 对于中间变量 z 的梯度,之前
h = ϕ ( z )
, 因此:
∂ J ∂ z = prod ( ∂ J ∂ h , ∂ h ∂ z ) = ∂ J ∂ h ⊙ ϕ ′ ( z ) .
因为激活函数
ϕ
是按元素计算的,所以计算梯度时,也需要按元素计算,此处使用符号
⊙
表示;
第七步:计算目标函数 J 对于权重参数
W ( 1 )
的梯度:
注意,到达
W ( 1 )
在计算图中有两个路径:
∂ J ∂ W ( 1 ) = prod ( ∂ J ∂ z , ∂ z ∂ W ( 1 ) ) + prod ( ∂ J ∂ s , ∂ s ∂ W ( 1 ) ) = ∂ J ∂ z x ⊤ + λ W ( 1 )
训练神经网络
前向传播需要存储计算结果(中间值),以便后续反向传播时能够读取。因此,训练比推理需要更多的内存。因为推理并不需要存储中间值。同时,如果训练的批量较大,意味着中间结果会很多,也容易造成内存不足。
数值稳定性和模型初始化
梯度消失和梯度爆炸
在反向传播的过程中,如果初始化函数或激活函数选择不当,容易造成梯度消失。有几种处理办法:
选择合适的激活函数,例如 ReLU;避免在深层网络中使用 Sigmoid 和 Tanh 等;
使用残差连接,将输入添加到输出中;
使用自适应学习率,以适配小梯度计算;
对输入进行归一化,以便让其落在激活函数的敏感区间;
权重初始化,保证激活值和梯度的方差稳定(合适的激活比率,以及相对平滑的梯度,而不是消失或爆炸)
神经网络学习的是函数,而不是参数。因为不同的参数,仍然可以得出相同的结果。这是因为模型本身自带的参数对称性。这种对称性包括:
置换对称性:交换任意两个隐藏神经元的权重和偏置,并同时在下一层交换输出,那么模型的表现不变;
缩放对称性:如果在某一层使用了“批量归一化”,那么不同尺度的参数,在经过这一层后,会得到同样的输出;缩放自由;
符号对称性:如果使用 sigmoid 或 tanh 激活函数,如果输入和输出的权重同时 取反,那么输出保持不变;
参数的对称性会导致优化收敛慢,因为存在多个等价的全局最小值;以下方法可减少参数对称性的影响:
随机初始化;
正则化;
归一化:例如 batchNorm, LayerNorm;
参数初始化
参数初始化非常非常重要,好的初始化参数能够极大的提高训练效率,不好的初始化参数会导致收敛缓慢甚至发散。例如过大的初始化参数,在经过多层网络放大后,容易出现参数爆炸;反之,如果初始化参数较小,则容易导致梯度消失。
Xavier 初始化
核心思路:让每一层输出的方差,尽量和输入的方差保持一致。
均匀分布 Xavier 实现:
权重从一个均匀分布 [-a, a] 中随机取样;
范围 a 的计算公式为:
a = 6 / ( f a n i n + f a n o u t )
f a n i n
和
f a n o u t
是输入和输出的神经元数量;
正态分布 Xavier 实现:
权重从一个均值为 0, 标准差为 std 的正态分布 N(0, std) 中采样;
标准差 std 的计算公式为:
s t d = 2 / ( f a n i n + f a n o u t )
Xavier 初始化主要适用于使用 Sigmoid 或 Tanh 激活函数的网络,因为这两个激活函数的敏感区域很小,因为需要使用 Xavier 将输入值保持在敏感区域附近;
He 初始化
核心思路:
保持前向传播每一层激活值的方差大致相同;
保持反向传播的梯度大致相同;
均匀分布的实现:
权重从一个均匀分布 [-a, a] 中随机取样;
范围 a 的计算公式为:
a = 6 / f a n i n
f a n i n
是输入的神经元数量;
正态分布实现:
权重从一个均值为 0, 标准差为 std 的正态分布 N(0, std) 中采样(第一步跟 Xavier 初始化一样);
标准差 std 的计算公式为:
s t d = 2 / f a n i n
He 初始化主要适用于 ReLU 激活函数,因为从理论上来说,ReLU 函数会将一半的输入置为 0,因为改变了信号的方差;常用于卷积神经网络、残差网络等;
环境和分布偏移
分布偏移的类型
协变量偏移
输入和输出的映射关系没有变,但输入的特征变了。例如使用真实猫和狗照片训练的模型,却遇到了卡通照片的输入;
标签偏移
与协变量刚好反过来,输入的特征没变,但是标签的分布变化了。例如服装销售,在夏天很多人购买泳装,模型总结了一系列与顾客相关的特征。但同一群顾客,特征不变,到了冬天的季节,却不购买泳装了。
概念偏移
我们根据销量,总结了当季流行的服饰的特征,用来判断一款服饰是否具备流行的元素。但是过了1-2年,流行的东西变了。原来流行的元素,已经不再流行了。
分布偏移纠正
对数几率回归,Logistic Regression,这名称看起来高大上,但其实就是 Sigmoid 函数,将输入映射到 [0, 1] 区间的函数而已;
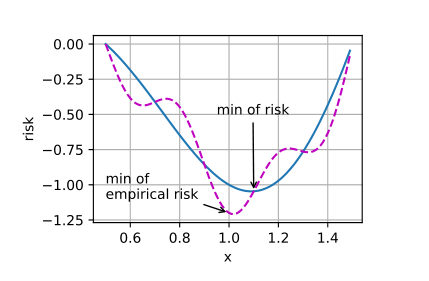
实际风险:模型在真实世界上运行时的平均损失;由于我们得不到真实世界的所有数据,所以这个风险只能是理论上的;
经验风险:模型在训练数据集上的平均损失;
学习问题的分类法
批量学习:最常见的方法,准备数据集,然后在此数据集上面进行批量训练;,训练好了后就部署。模型参数是静态的。部署后不再更新;
在线学习:每天不断将预测结果加到学习的数据集中,不断的迭代更新模型;
实战 Kaggle 比赛
数据预处理
样本某个特征的缺失值,替换为该特征的平均值;
标准化数据:将样本缩放到零均值和单位方差,以便将不同的特征,放在一个相同的尺度上;
x = x − μ σ
其中:
μ
为均值,
σ
为标准差
标准化完数据后,因为此时的均值变成了 0 ,所以原本缺失的特征值,都可以初始化为 0;
离散值使用独热编码进行转换;
可考虑先使用线性模型进行训练,看是否能够得到比随机猜测更好的结果。如果不能,说明数据本身有问题。
深度学习计算
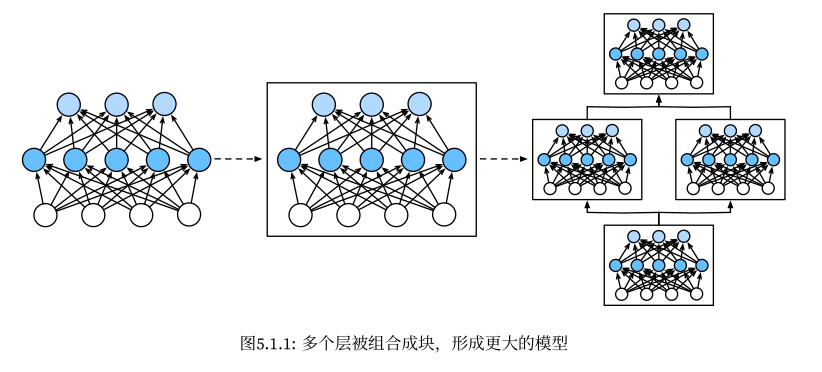
层和块
神经元和层是基本的单位,但在构建深度模型时,这个单位仍然过于底层了。于是引入了块,它的抽象层级介于层和模型之间,一个块可由单个或多个层构成。一个模型可由多个块组成。不同块之间可以是上下级的关系,也可以是平行的关系。
在编程实践中,可使用 Class 类来抽象一个块;
自定义块
每个块需要具备的功能:
将输入数据作为前向传播的参数;
通过前向传播生成输出;
计算输出相对于输入的梯度;
存储所需要的参数;
可初始化模型参数;
1 2 3 4 5 6 7 8 9 10 11 12 import torchfrom torch import nnfrom torch.nn import functional as Fclass MLP (nn.Module):def __init__ (self ):super ().__init__()self .hidden = nn.Linear(20 , 256 )self .out = nn.Linear(256 , 10 )def forward (self, X ):return self .out(F.relu(self .hidden(X)))
此处使用了内置的 nn.Linear 来实例化全链接层,它内置了默认的反向传播函数和参数初始化功能。
顺序块
1 2 3 4 5 6 7 8 9 10 11 12 13 class MySequential (nn.Module):def __init__ (self, *args ):super ().__init__()for idx, module in enumerate (args):self ._modules[str (idx)] = module def forward (X ):for block in self ._modules.values():return X20 , 256 ), nn.ReLU(), nn.Linear(256 , 10 ))
执行代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class FixedHiddenMLP (nn.Module):def __init__ (self ):super ().__init__()self .rand_weight = torch.rand((20 , 20 ), requires_grad=False )self .linear = nn.Linear(20 , 20 )def forward (self, X ):self .linear(X)self .rand_weight) + 1 )self .linear(X)while X.abs ().sum () > 1 :2 return X.sum ()
1 2 3 4 5 6 7 8 9 10 11 12 13 class NestMLP (nn.Module):def __init__ (self ):super ().__init__()self .net = nn.Sequential(nn.Linear(20 , 64 ), nn.ReLU(),64 , 32 ), nn.ReLU())self .linear(32 , 16 )def forward (self, X ):return self .linear(self .net(X))16 , 20 ), FixedHiddelMLP())
效率
Python 由于不方便并行运算,因此,当计算量比较大的时候,需要 GPU 出马。
参数管理
找到合适的参数,以便让损失值最小化是我们的目标。经过训练找到这些参数后,我们需要保存参数,以便后续预测时能够复用。另外,我们也需要能够读取参数,以便能够可视化,以及对参数进行检查。
1 2 3 4 5 6 import torchfrom torch import nn4 , 8 ), nn.ReLU(), nn.Linear(8 , 1 ))2 , 4 ))
参数访问
1 2 3 4 5 6 print (net[2 ].state_dict())
访问目标参数
1 2 3 4 print (type (net[2 ].bias))print (net[2 ].bias)print (net[2 ].bias.data)print (net[2 ].bias.grad)
1 2 3 4 5 <class 'torch.nn.parameter.Parameter'>
一次性访问所有参数
1 2 print (*[(name, param.shape) for name, param in net[0 ].named_parameters()])print (*[(name, param.shape) for name, param in net.named_parameters()])
1 2 ('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
从嵌套块读取参数
1 2 3 4 5 6 7 8 9 10 11 12 13 def block1 ():return nn.Sequential(nn.Linear(4 , 8 ), nn.ReLU(),8 , 4 ), nn.ReLU())def block2 ():for i in range (4 ):f'block {i} ' , block1())return net4 , 1 ))
1 2 tensor([[-0.3078],
1 rgnet[0 ][1 ][0 ].bias.data
1 tensor([-0.2539, 0.4913, 0.3029, -0.4799, 0.2022, 0.3146, 0.0601, 0.3757])
参数初始化
默认情况下,PyTorch 会自动初始化,使用随机参数值,基于输入和输出维度,例如 Xavier 初始化、He 初始化;
内置初始化
1 2 3 4 5 6 7 def init_normal (m ):if type (m) == nn.Linear:0 , std=0.01 )0 ].weight.data[0 ], net[0 ].bias.data[0 ]
1 (tensor([-0.0128, -0.0141, 0.0062, 0.0028]), tensor(0.))
也可以初始化为给定的常数
1 2 3 4 5 6 7 def init_constant (m ):if type (m) == nn.Linear:1 )0 ].weight.data[0 ], net[0 ].bias.data[0 ]
1 (tensor([1., 1., 1., 1.]), tensor(0.))
不同的块可以使用不同的初始化方法
1 2 3 4 5 6 7 8 9 10 11 12 13 def init_xavier (m ):if type (m) == nn.Linear:def init_42 (m ):if type (m) == nn.Linear:42 )0 ].apply(init_xavier)2 ].apply(init_42)print (net[0 ].weight.data[0 ])print (net[2 ].weight.data)
1 2 tensor([ 0.3809, 0.5354, -0.4686, -0.2376])
自定义初始化
1 2 3 4 5 6 7 8 9 10 11 12 13 def my_init (m ):if type (m) == nn.Linear:print ("Init" , *[(name, param.shape) for name, param in m.named_parameters()][0 ])10 , 10 )abs () >= 5 0 ].weight[:2 ]
1 2 3 4 5 Init weight torch.Size([8, 4])
1 2 3 4 0 ].weight.data[:] += 1 0 ].weight.data[0 , 0 ] = 42 0 ].weight.data[0 ]
1 tensor([42.0000, 10.3334, 6.0616, 9.3095])
参数绑定
1 2 3 4 5 6 7 8 9 10 11 12 13 8 , 8 )4 , 8 ), nn.ReLU(),8 , 1 ))print (net[2 ].weight.data[0 ] == net[4 ].weight.data[0 ])2 ].weight.data[0 , 0 ] = 100 print (net[2 ].weight.data[0 ] == net[4 ].weight.data[0 ])
1 2 tensor([True, True, True, True, True, True, True, True])
复用的这一层,在反向传播时,梯度会叠加;
延后初始化
PyTorch 的默认行为是 nn.Module 在实例化时,会马上自动初始化参数(使用 Xavier 方法),暂时不清楚这里写的延后初始化是什么意思?
除非在定义 Module 时,显示指定某个层为 None,这样由于不知道该层的维度参数,因为无法自动初始化参数,需要后续调用 forward 方法时,根据传入的数据自动初始化参数;示例如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class FlexibleModel (nn.Module):def __init__ (self ):super ().__init__()self .conv = nn.Conv2d(3 , 16 , 3 )self .fc = None def forward (self, x ):self .conv(x)if self .fc is None :0 ), -1 ).shape[1 ]self .fc = nn.Linear(n_features, 10 ).to(x.device)0 ), -1 )self .fc(x)return x
自定义层
不带参数的层
1 2 3 4 5 6 7 8 9 10 import torchimport torch.nn.functional as Ffrom torch import nnclass CenteredLayer (nn.Module):def __init__ (self ):super ().__init__()def forward (self, X ):return X - X.mean()
虽然该层不携带参数,但是它可以做为一种计算机制,与其他块组合起来协同工作
1 net = nn.Sequential(nn.Linear(8 , 128 ), CenteredLayer())
没有参数的层,意味着在训练的过程中,这一层没有需要更新的参数;
带参数的层
1 2 3 4 5 6 7 8 9 10 11 12 13 class MyLinear (nn.Module):def __init__ (self, in_units, units ):super ().__init__()self .weight = nn.Parameter(torch.randn(in_units, units))self .bias = nn.Parameter(torch.randn(units,))def forward (self, X ):self .weight.data) + self .bias.datareturn F.relu(linear)5 , 3 )
1 2 3 4 5 6 Parameter containing:
1 2 X = torch.rand(2 , 5 )
1 2 tensor([[0.0984, 0.5687, 2.8316],
自定义的 Linear 可以组合到 Sequential 中
1 2 net = nn.Sequential(MyLinear(64 , 8 ), MyLinear(8 , 1 ))2 , 64 ))
1 2 tensor([[7.5465],
读写文件
加载和保存张量
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import torchfrom torch import nnfrom torch.nn import functional as F4 )'x-file' )'x-file' )4 )'x-files' )'x-files' )'x' : x, 'y' : y}'mydict' )'mydict' )
加载和保存模型参数
由于模型中可能包含任意的代码,因此模型本身难以保存,只能保存模型的参数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class MLP (nn.Module):def __init__ (self ):super ().__init__()self .hidden = nn.Linear(20 , 256 )self .output = nn.Linear(256 , 10 )def forward (self, X ):return self .output(F.relu(self .hidden(X)))2 , 20 ))"mlp.params" )'mlp.params' ))eval ()
GPU
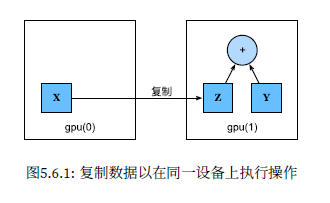
计算设备
1 2 3 4 5 6 7 8 'cuda' ) 'cuda:1' )
1 2 3 4 5 6 7 8 9 def try_gpu (i=0 ):if torch.cuda.device_count() >= i + 1 :return torch.device(f'cuda:{i} ' )return torch.device('cpu' )def try_all_gpus ():f'cuda:i' ) for i in range (torch.cuda.device_count())]return devices if devices else [torch.device('cpu' )]
张量与GPU
1 2 3 1 , 2 , 3 ])
1 2 3 4 5 2 , 3 , device=try_gpu())2 , 3 , device=try_gpu(1 ))
如果两个张量存储在不同的设备,则需要先复制到同一设备后,才能计算
神经网络与GPU
模型也可以指定设备
1 2 3 net = nn.Sequential(nn.Linear(3 , 1 ))
1 2 tensor([[-0.4275],'cuda:0' , grad_fn=<AddmmBackward0>)
1 net[0 ].weight.data.device
1 device(type ='cuda' , index=0)
卷积神经网络
从全连接到卷积
多层感知机很适合用来处理类似表格类型的数据,表格的每一行代表一个样本,每一列代表样本的一种属性。我们通过全连接寻找特征之间的交互关系。
如果特征数较小,全连接计算是可行的。但如果特征数很多,例如一张图片有上百万像素,即使只设置 1000 个隐藏单元,都将涉及
10 6 ∗ 10 3 = 10 9
个参数,这个计算量太可怕了,需要耗费巨大的计算资源,而且效果还不一定理想。因为要拟合这么多的参数,训练的数据集也需要十分庞大才行。
为了应对图像识别的问题,我们需要寻找新的方法。由于图像中的物体是包含结构的,因为我们可尝试先提取其中的结构,再进行相互关系的计算。
不变性
同一个位置,不管它处于图片中的哪个位置,仍然还是这个物体本身,而不会变成另外一个物体。因此,我们可以说,物体在图像中具有空间不变性 spatial invariance,它包括:
平移不变性 translattion invariance:不管物体在哪个位置,提取出来的特征都是相同的;
局部性 locality:先从探索局部开始,如果没找到,再聚合探索更大的区域;
多层感知机的限制
多层感知机由于是全接的,不方便从局部区域中提取结构关系;同时,因为是全连接,导致 MLP 容易出现参数爆炸。
相比于 MLP,卷积神经网络需要的参数量很少,因为它专注于局部计算即可。局部计算能够成立的前提,是数据本身包含平移不变性。同一个局部数据,不管它出现在整体中的那个局部,参数都能够产生效果。如果数据不包含平移不变性,那么很可能局部卷积计算将得出不同的结果,最终模型不具备泛化能力。
图像卷积
互相关运算
滑动窗口的互相关计算
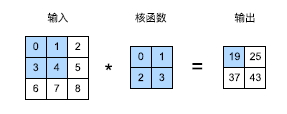
1 2 3 4 5 6 7 8 9 10 11 import torchfrom torch import nnfrom d2l import torch as d2ldef corr2d (X, K ):0 ] - h + 1 , X.shape[1 ] - w + 1 )for i in range (Y.shape[0 ]):for j in range (Y.shape[1 ]):sum ()return Y
卷积层
卷积层涉及两个运算,一个是卷积核的计算,一个是偏置的计算。因为卷积层的训练,实际上就是找到合适参数的卷积核和偏置标量;
1 2 3 4 5 6 7 8 class Conv2D (nn.Module):def __init__ (self, kernel_size ):super ().__init__()self .weight = nn.Parameter(torch.rand(kernel_size))self .bias = nn.Parameter(torch.zeros(1 )) def forward (self, X ):return corr2d(x, self .weight) + self .bias
图像中目标的边缘检测
1 2 3 4 6 , 8 ))2 :6 ] = 0
1 2 3 4 5 6 tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
1 2 3 4 1.0 , -1.0 ]])
1 2 3 4 5 6 7
学习卷积核
问:如何知道应该使用什么样的卷积核?
答:针对不同的问题有不同的答案。因此比较理想的做法,是让模型自己学习合适的卷积核参数。一开始可先随机初始化,然后每一轮迭代,对比模型输出与目标值的损失,通过反向传播和梯度计算,不断更新卷积核参数,让损失最小化。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 ,1 , kernel_size=(1 , 2 ), bias=False )1 , 1 , 6 , 8 ))1 , 1 , 6 , 7 ))3e-2 for i in range (10 ):2 sum ().backward()if (i + 1 ) % 2 == 0 :print (f'epoch {i+1 } , loss {l.sum ():.3 f} ' )
1 2 3 4 5 epoch 2, loss 6.422
1 2 1 , 2 ))
1 tensor([[ 1.0010, -0.9739]])
互相关和卷积
CNN 中“卷积层”的计算,其实是互相关计算。互相关计算与卷积计算的区别在于,卷积计算在运算前,会翻转滤波器(翻转180度);
假设有一个输入信号 [a, b, c],有一个滤波器 [x, y]
互相关计算不翻转滤波器,直接做滑动窗口计算,即:
[a, b] * [x, y]
[b, c] * [x, y]
结果为 [a*x + b*y, b*x + c*y]
卷积计算则先翻转滤波器,将其变成 [y, x],然后接下来再做互相关计算:
[a, b] * [y, x]
[b, c] * [y, x]
结果为 [a*y + b*x, b*y + c*x]
互相关计算的一种应用在于放大匹配信号。例如某张图片中的某个局部区域,包含一个头像;此时如果使用一个头像滤波器去扫描这张图像时,在该局部区域由于二者的信号类似,因此会出现最大响应,从而帮助我们找到图片中的头像位置。这也是为什么该计算称为互相关计算的原因。相关性越强,计算结果的值越大。
特征映射和感受野
从输入到卷积层的输出,有点像是一种特征映射。卷积核的作用有点像是特征提取器。
对于某一层中的某个元素 x,它来自于前面各层的卷积计算。所有前面各层参与计算 x 的元素,称为 x 的感受野。
填充和步幅
假设输入的形状为
n h × n k
,卷积核的形状为
k h × k w
,那么最终输出的形状为
( n h − k h + 1 ) × ( n w − k w + 1 )
通过填充或者修改步幅,可以改变输出的形状。
填充
如果不做任何处理,那么每一次卷积,都会丢失一些边缘信息。为避免这个情况,我们可以在卷积计算前,先对数据进行边缘的填充(通常填充0);
填充可以让输出和输入保持相互的形状,这也是为什么卷积核形状通常取奇数的原因。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import torchfrom torch import nndef comp_conv2d (conv2d, X ):1 , 1 ) + X.shape)return Y.reshape(Y.shape[2 :])1 , 1 , kernel_size=3 , padding=1 )8 , 8 ))
1 2 3 1 , 1 , kernel_size=(5 , 3 ), padding=(2 , 1 ))
步幅
假设垂直步幅为
s h
、水平步幅为
s w
,则输出形状为:
⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ .
假设
p h = k h − 1
和
p w = k w − 1
,同时设置步幅可以被输入和输出的高度整除,则公式可以简化如下:
( n h / s h ) × ( n w / s w )
1 2 3 1 , 1 , kernel_size=3 , padding=1 , stride=2 )
在实际业务中,垂直和水平的填充和步幅值一般是一样的。
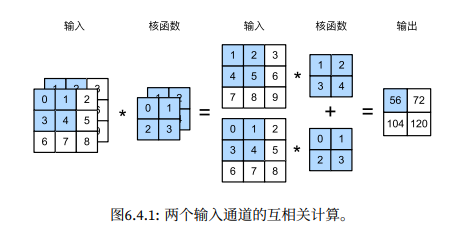
多输入多输出通道
多输入通道
假设输入有 2 个通道,那么卷积核也相应有 2 个通道。每个通道的计算结果,最后进行累加,即可得到单输出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchfrom d2l import torch as d2ldef corr2d_multi_in (X, K ):return sum (d2l.corr2d(x, k) for x, k in zip (X, K))0.0 , 1.0 , 2.0 ], [3.0 , 4.0 , 5.0 ], [6.0 , 7.0 , 8.0 ]],1.0 , 2.0 , 3.0 ], [4.0 , 5.0 , 6.0 ], [7.0 , 8.0 , 9.0 ]]])0.0 , 1.0 ], [2.0 , 3.0 ]], [[1.0 , 2.0 ], [3.0 , 4.0 ]]])
1 2 tensor([[ 56., 72.],
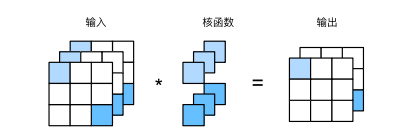
多输出通道
除了单输出,也可以多输出。理论上可以设置任意多的输出通道,但这会显著增加参数量和计算量,但模型性能并不一定有提升,反而有可能容易过拟合。
我们在初始卷积层的时候,只传入了卷积核的尺寸,并没有设置卷积核的数量。事实上,卷积核的数量是根据输出通道来的。有多少个输出通道,就有多少个卷积核。这也意味着参数数量等比例增长。
每个卷积核都对应一个要学习的特征,如果有效提取该特征,则依赖于卷积核的参数。该参数正是训练过程中要学习的目标,它通过反向传播不断调整,直到找到最佳值。
输出通道可以比输入通道多,也可以比输入通道少,它可以是任意的数量。当它比输入通道多的时候,就是在解析出更多的细分特征。当它比输入通道少时,就是合并输入通道,常用于最后一层。
1 2 3 4 5 6 7 8 def corr2d_multi_in_out (X, K ):return torch.stack([corr2d_multi_in(X, k) for k in K], 0 )1 , K + 2 ), 0 )
1 torch.Size([3, 2, 2, 2])
1 corr2d_multi_in_out(X, K)
1 2 3 4 5 6 7
###
1 × 1
卷积层
1 × 1
的卷积核,由于只作用于单个像素,因此它并不具备从局部区域的多个像素中提取特征的能力。但是它有个作用是可以提取多个通道之间的特征,相当于多个通道之间的一次全连接计算,这在某些场景下是一个有用的功能。例如可用来调整通道数量,或者可以调整模型的复杂度。
以上是一个双通道输出的
1 × 1
卷积核,有多少个输出通道,就需要有多少个核函数。每个核函数负责从输入通道中读取特征信息。有多个输出通道,也就意味着提取多个特征。假设有 3 个输出通道,表面上看和输入通道数量是一样的。但背后的含义已经发生了变化,3 个输出通道分别代表从输入数据提取的特征,它的含义已经和输入不同。当然,某些极端情况下,也有可能相同。例如输入的 3 个通道分别代表红绿蓝,搞不好输出也可以仍然代表这个信息,取决于训练过程中,参数如何调整变化。
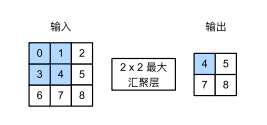
汇聚层
此处汇聚层对应的英文是 pooling,之前看 Keras 时,翻译为“池化层”;
最大汇聚层和平均汇聚层
汇聚层也是使用滑动窗口,但是它与卷积运算的区别在于,它不做卷积计算,而是作池化计算,例如取最大化,或者取平均值。
最大汇聚的一个好处是,即使特征值在原始图像中发生了偏移,它最终映射到汇聚层后的结果是不变的。这样就实现了平移不变性。
汇聚是一个降采样的计算,它会改变张量的高度和宽度,但通常不会改变通道数。
形状变化如下:
输 出 尺 寸 输 入 尺 寸 输出尺寸 = ⌊ 输入尺寸 + 2 × padding − kernel_size stride + 1 ⌋
不同汇聚类型的输出形状:
汇聚类型
输入形状
典型参数
输出形状
MaxPool2d[B, C, H, W]kernel_size=2, stride=2[B, C, H/2, W/2]
AdaptiveAvgPool2d[B, C, H, W]output_size=(16, 16)[B, C, 16, 16]
GlobalAvgPool2d[B, C, H, W]-
[B, C, 1, 1]
填充与步幅
我们同样可以使用填充和步幅来调整输出的形状。默认情况下,汇聚使用的步幅和滑动汇聚窗口的大小是一致的。
多通道
每个通道在进行汇聚计算时,计算结果是独立的。这意味着输入有多少个通道,那么输出也有相同的通道数量。它不像卷积层计算会合并多个通道的值。
卷积神经网络
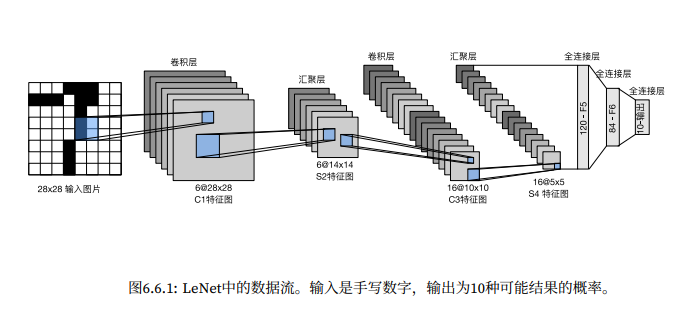
LeNet
LeNet 由于研发时间较早,它的结构较为简单。它采用了卷积层、sigmoid 激活函数和平均汇聚层。
后来发现使用最大汇聚层 + ReLU 激活函数效果会更好。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchfrom torch import nnfrom d2l import torch as d2l1 , 6 , kernel_size=5 , padding=2 ), nn.Sigmoid(), 2 , stride=2 ), 6 , 16 , kernel_size=5 ), nn.Sigmoid(), 2 , stride=2 ), 16 * 5 * 5 , 120 ), nn.Sigmoid(), 120 , 84 ), nn.Sigmoid(), 84 , 10 ))
模型训练
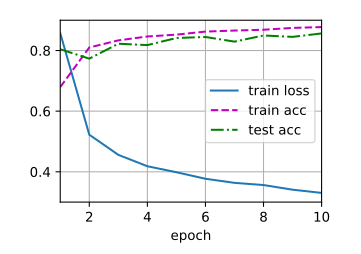
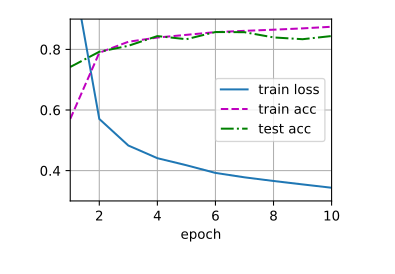
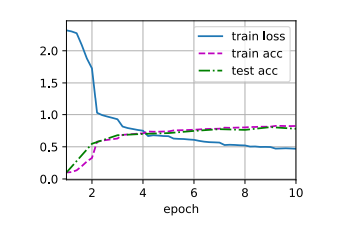
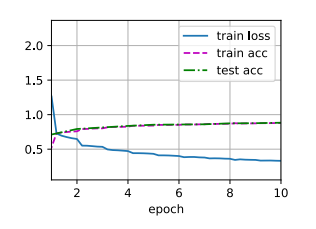
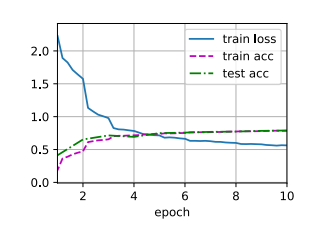
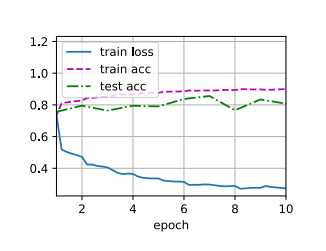
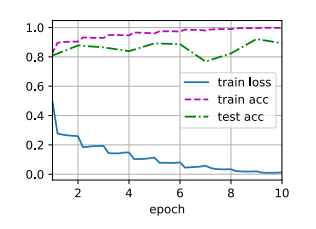
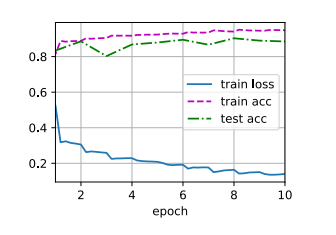
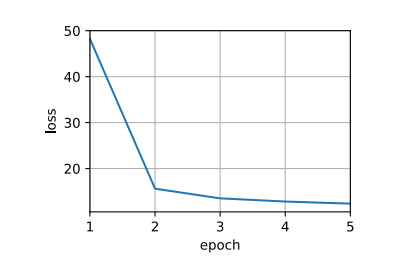
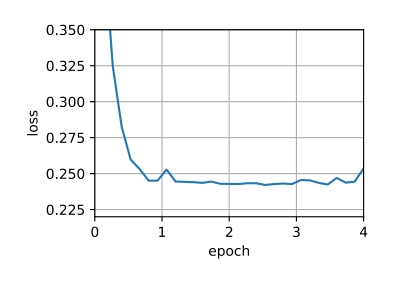
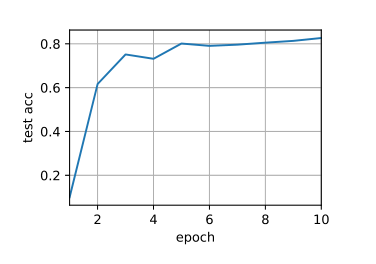
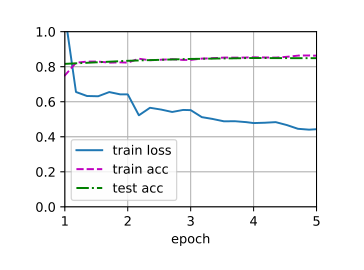
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 def evaluate_accuracy_gpu (net, data_iter, device=None ): if isinstance (net, nn.Module):eval () if not device:next (iter (net.parameters())).device2 )with torch.no_grad():for X, y in data_iter:if isinstance (X, list ):for x in X]else :return metric[0 ] / metric[1 ]def train_ch6 (net, train_iter, test_iter, num_epochs, lr, device ):def init_weights (m ):if type (m) == nn.Linear or type (m) == nn.Conv2d:print ('training on' , device)'epoch' , xlim=[1 , num_epochs],'train loss' , 'train acc' , 'test acc' ])len (train_iter)for epoch in range (num_epochs):3 )for i, (X, y) in enumerate (train_iter):with torch.no_grad():0 ], d2l.accuracy(y_hat, y), X.shape[0 ])0 ] / metric[2 ]1 ] / metric[2 ]if (i + 1 ) % (num_batches // 5 ) == 0 or i == num_batches - 1 :1 ) / num_batches,None ))1 , (None , None , test_acc))print (f'loss {train_l:.3 f} , train acc {train_acc:.3 f} , ' f'test acc {test_acc:.3 f} ' )print (f'{metric[2 ] * num_epochs / timer.sum ():.1 f} examples/sec ' f'on {str (device)} ' )256 0.9 , 10
1 2 3 loss 0.467, train acc 0.825, test acc 0.821
现代卷积神经网络
卷积神经网络的原理是简单的,但如何组合它们,以便实现性能最大化,却是一个不断试错的过程。它更像是一种艺术,需要一定直觉和反复的尝试。在过去的 10 几年中,研究人员逐渐找到了一些行之有效的卷积网络结构。
深度卷积神经网络 AlexNet
学习表征
计算机视觉研究人员早期主要侧重于特征提取算法,虽然当时已有研究者提出特征提取也是可以被学习的,但当时外部条件还不具备,该想法还无法验证和落地,一是因为缺少足够的标注数据,二是缺少算力。
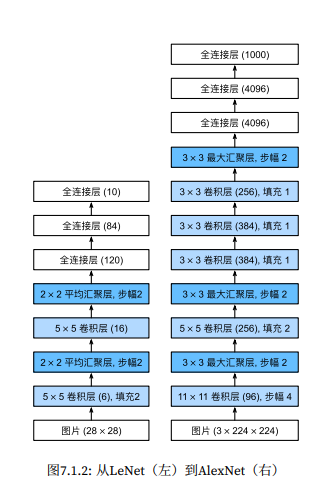
AlexNet
AlexNet 的基本结构和 LeNet 有些类似:
AlexNet 使用了一些新的技术:
激活函数改用 ReLU
深度更深,通道数量更多;
全连接层的维度非常多,有 4096(这导致该层的参数规模非常庞大,需要更多的显存);
使用了数据增强,让数据集更大,提升模型的泛化能力;
在全连接层使用了 Dropout;
平均汇聚改为最大汇聚;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import torchfrom torch import nnfrom d2l import torch as d2l1 , 96 , kernel_size=11 , stride=4 , padding=1 ), nn.ReLU(),3 , stride=2 ),96 , 256 , kernel_size=5 , padding=2 ), nn.ReLU(),3 , stride=2 ),256 , 384 , kernel_size=3 , padding=1 ), nn.ReLU(),384 , 384 , kernel_size=3 , padding=1 ), nn.ReLU(),384 , 256 , kernel_size=3 , padding=1 ), nn.ReLU(),3 , stride=2 ),6400 , 4096 ), nn.ReLU(),0.5 ), 4096 , 4096 ), nn.ReLU(),0.5 ), 4096 , 10 ))
1 2 3 4 5 X = torch.randn(1 , 1 , 224 , 224 )for layer in net:print (layer.__class__.__name__,'output shape:\t' ,X.shape)
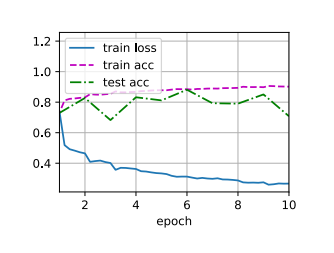
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Conv2d output shape: torch.Size([1, 96, 54, 54])
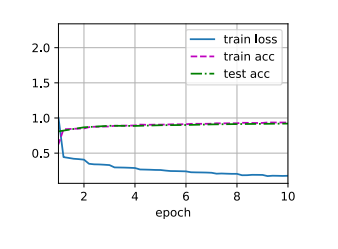
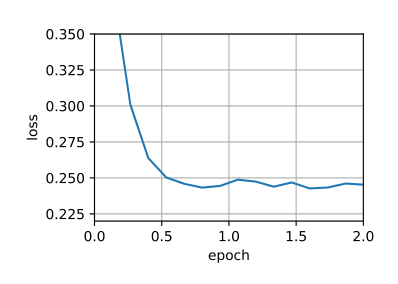
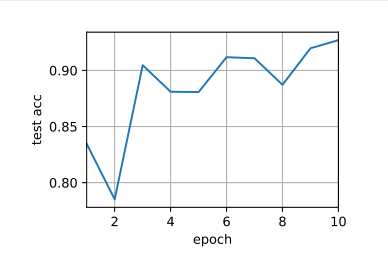
1 2 3 4 5 batch_size = 128 224 )0.01 , 10
1 2 3 loss 0.326, train acc 0.881, test acc 0.879
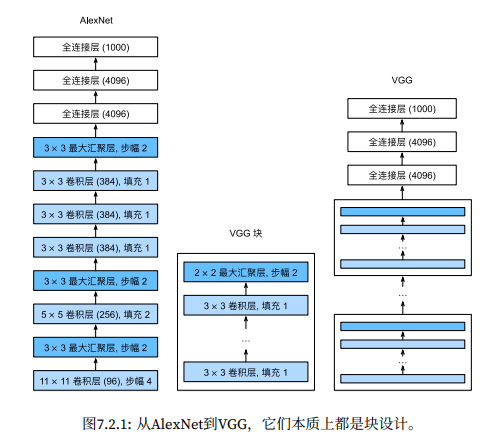
使用块的网络 VGG
VGG 的全称是 Visual Geometry Group,是牛津大学的视觉几何组,他们提出了“块”的理念。块相当于对若干个层进行组合的一个抽象单位。这样人们在设计模型时,可以使用“块”的单位来构建,而不用从最底层的“层”入手。
VGG 块
1 2 3 4 5 6 7 8 9 10 11 12 13 import torchfrom torch import nnfrom d2l import torch as d2ldef vgg_block (num_convs, in_channels, out_channels ):for _ in range (num_convs):3 , padding=1 ))2 , stride=2 ))return nn.Sequential(*layers)
out_channels 参数是可以手工任意指定的,它表示要从输入中提取多少特征。这个值并不是越大越好,如果太大,会显著增加训练的时间,模型参数量也会变大,但模型性能却不一定更好。一般随着深度的增加,每一层的 out_channels 也会相应增加。以便从输入的数据解析出更多的特征信息。
VGG 网络
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def vgg (conv_arch ):1 for (num_convs, out_channels) in conv_arch:return nn.Sequential(7 * 7 , 4096 ), nn.ReLU(), nn.Dropout(0.5 ),4096 , 4096 ), nn.ReLU(), nn.Dropout(0.5 ),4096 , 10 )1 , 64 ), (1 , 128 ), (2 , 256 ), (2 , 512 ), (2 , 512 ))1 , 1 , 224 , 224 ))for blk in net:print (blk.__class__.__name__,'output shape:\t' ,X.shape)
1 2 3 4 5 6 7 8 9 10 11 12 13 Sequential output shape: torch.Size([1, 64, 112, 112])
训练模型
1 2 3 4 5 6 7 ratio = 4 0 ], pair[1 ] // ratio) for pair in conv_arch]0.05 , 10 , 128 224 )
1 2 3 loss 0.220, train acc 0.918, test acc 0.900
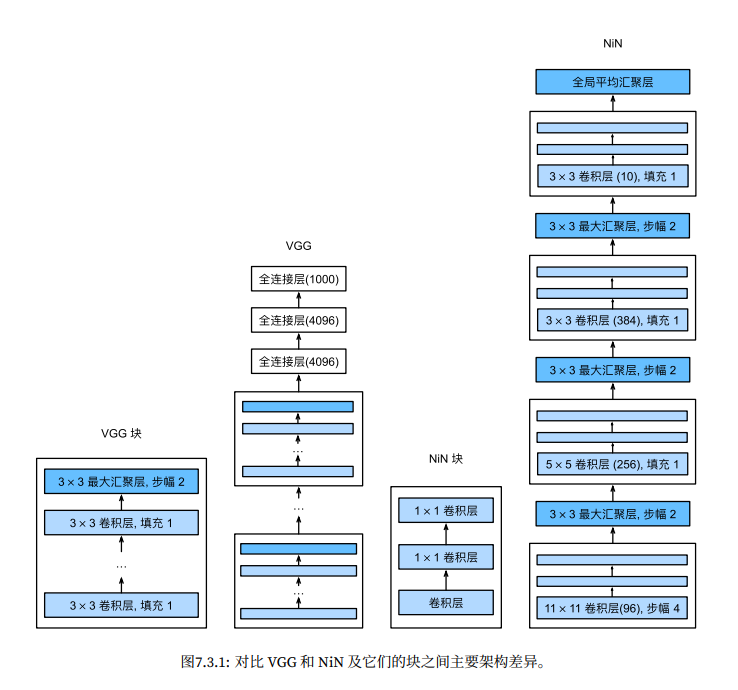
网络中的网络 NiN
NiN 块
NiN 块有点类似 VGG 块,区别在于它在卷积层和汇聚层之间,插入了两个
1 × 1
的卷积层。这两个
1 × 1
的卷积层充当全连接的作用,作用于单个像素的不同通道,计算通道间的特征关系。然后再进入汇聚层过滤。
另外还有一个区别是拿掉了最后的三个全连接层。因为每个块里面,已经各做过两个全连接计算了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchfrom torch import nnfrom d2l import torch as d2ldef nin_block (in_channels, out_channels, kernel_size, strides, padding ):return nn.Sequential(1 ),1 ),
NiN 模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 net = nn.Sequential(1 , 96 , kernel_size=11 , strides=4 , padding=0 ),3 , stride=2 ),96 , 256 , kernel_size=5 , strides=1 , padding=2 ),3 , stride=2 ),256 , 384 , kernel_size=3 , strides=1 , padding=1 ),3 , stride=2 ),0.5 ),384 , 10 , kernel_size=3 , strides=1 , padding=1 ),1 , 1 )),
1 2 3 4 X = torch.rand(size=(1 , 1 , 224 , 224 ))for layer in net:print (layer.__class__.__name__,'output shape:\t' , X.shape)
1 2 3 4 5 6 7 8 9 10 Sequential output shape: torch.Size([1, 96, 54, 54])
训练模型
1 2 3 lr, num_epochs, batch_size = 0.1 , 10 , 128 224 )
1 2 3 loss 0.322, train acc 0.881, test acc 0.865
相比 AlexNet 和 VGG,NiN 移除了最后的三个全连接层,大幅减少了参数数量,因此避免了过拟合的风险。
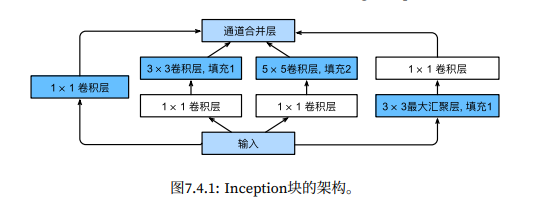
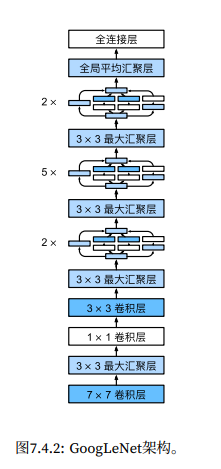
含并行连结的网络 GoogleNet
GoogleNet 的特别之处在于,它组合不同尺寸的卷积核,最后合并它们的计算结果。并证明了这种组合的性能表现,要优于之前的 NiN 块。NiN 是没有组合的,它只使用了单一尺寸的卷积核。
Inception 块
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import torchfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2lclass Inception (nn.Module):def __init__ (self, in_channels, c1, c2, c3, c4, **kwargs ):super (Inception, self ).__init__(**kwargs)self .p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1 )self .p2_1 = nn.Conv2d(in_channels, c2[0 ], kernel_size=1 )self .p2_2 = nn.Conv2d(c2[0 ], c2[1 ], kernel_size=3 , padding=1 )self .p3_1 = nn.Conv2d(in_channels, c3[0 ], kernel_size=1 )self .p3_2 = nn.Conv2d(c3[0 ], c3[1 ], kernel_size=5 , padding=2 )self .p4_1 = nn.MaxPool2d(kernel_size=3 , stride=1 , padding=1 )self .p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1 )def forward (self, x ):self .p1_1(x))self .p2_2(F.relu(self .p2_1(x))))self .p3_2(F.relu(self .p3_1(x))))self .p4_2(self .p4_1(x)))return torch.cat((p1, p2, p3, p4), dim=1 )
卷积核有点像一个特征探测器(滤波器),当使用不同尺寸的探测器时,它就有可能探测出不同的特征。类似于近看和眼看捕捉到的特征不同。
GoogleNet 模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 1 , 64 , kernel_size=7 , stride=2 , padding=3 ),3 , stride=2 , padding=1 ),64 , 64 , kernel_size=1 ),64 , 192 , kernel_size=3 , padding=1 ),3 , stride=2 , padding=1 )192 , 64 , (96 , 128 ), (16 , 32 ), 32 ),256 , 128 , (128 , 192 ), (32 , 96 ), 64 ),3 , stride=2 , padding=1 )480 , 192 , (96 , 208 ), (16 , 48 ), 64 ),512 , 160 , (112 , 224 ), (24 , 64 ), 64 ),512 , 128 , (128 , 256 ), (24 , 64 ), 64 ),512 , 112 , (144 , 288 ), (32 , 64 ), 64 ),528 , 256 , (160 , 320 ), (32 , 128 ), 128 ),3 , stride=2 , padding=1 )832 , 256 , (160 , 320 ), (32 , 128 ), 128 ),832 , 384 , (192 , 384 ), (48 , 128 ), 128 ),1 ,1 )),1024 , 10 ))
1 2 3 4 X = torch.rand(size=(1 , 1 , 96 , 96 ))for layer in net:print (layer.__class__.__name__,'output shape:\t' , X.shape)
1 2 3 4 5 6 Sequential output shape: torch.Size([1, 64, 24, 24])
GoogleNet 模型相当复杂,各个 Inception 块之间的连接,需要手工计算好输入和输出的通道数。目前使用的各层通道数及比例,是经过大量反复试错后得来的。
每个 Inception 块类似一个子模块,该子模型有 4 条路径。每条路径使用不同尺寸的卷积核,来从输入的数据中提取特征信息。同时还使用
1 × 1
的卷积来合并通道数据,避免参数太多,减少复杂度。
训练模型
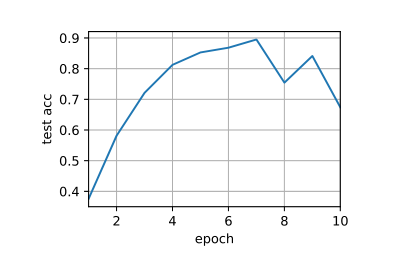
1 2 3 lr, num_epochs, batch_size = 0.1 , 10 , 128 96 )
1 2 3 loss nan, train acc 0.100, test acc 0.100
批量规范化
如果没有使用一些合理的技术,在训练深度神经网络时,会发现模型很难收敛,总是在振荡。后来人们找到了一些能够帮助收敛的技术,例如批量规范化。
训练深层网络
在模型前向传播过程中,虽然一开始的输入已经规范化了,但输入数据与权重参数的计算,会让原本的规范化消失。此时需要重新进行规范化。
批量规范化会让数据减去总体的平均值再除以标准差,因此每个批量的样本数不得为 1,不然平均值是样本本身,规范化变成了 0,这样就没法训练了。因此,选择合适的批量大小很重要。
规范化后,数据的平均值为 0,单位方差为 1;之后引入拉伸参数 scale 和偏移参数 shift,让模型进行学习。以便让数据更好的映射现实中的特征。
BN ( x ) = γ ⊙ x − μ ^ B σ ^ B + β
其中:
*
γ
是拉伸参数;
β
是偏移参数;
σ ^
是小批量的标准差;
μ ^
是小批量的平均值;
μ ^ B = 1 | B | ∑ x ∈ B x , σ ^ B 2 = 1 | B | ∑ x ∈ B ( x − μ ^ B ) 2 + ϵ .
批量规范化层
全连接层和卷积层的批量规范化有些不同。
全连接层
h = ϕ ( BN ( W x + b ) )
其中:
ϕ
是激活函数
卷积层
卷积计算的场景,不像全连接计算的二维数据,而是可能有多个输出通道。因此每个通道需要单独规范化,有自己的参数(拉伸和偏移);并且此时小批量的平均值,是按所有样本的每个通道中所有空间位置的值进行计算的。
预测场景
在预测场景下,批量规范化与训练也有所不同。一个是不需要添加噪声,二是不需要计算小批量的样本方差
从零实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import torchfrom torch import nnfrom d2l import torch as d2ldef batch_norm (X, gamma, beta, moving_mean, moving_var, eps, momentum ):if not toch.is_grad_enabled(): else : assert len (X.shape) in (2 , 4 )if len (X.shape) == 2 : 0 )2 ).mean(dim=0 )else :0 , 2 , 3 ), keepdim=True ) 2 ).mean(dim=(0 , 2 , 3 ), keepdim=True )1.0 - momentum) * mean1.0 - momentum) * varreturn Y, moving_mean.data, moving_var.data
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class BatchNorm (nn.Module):def __init__ (self, num_features, num_dims ):super ().__init__()if num_dims == 2 :1 , num_features)if num_dims == 4 :1 , num_features, 1 , 1 )self .gamma = nn.Parameter(torch.ones(shape))self .beta = nn.Parameter(torch.zeros(shape))self .moving_mean = torch.zeros(shape)self .moving_var = torch.ones(shape)def forward (self, X ):if self .moving_mean.device != X.device:self .moving_mean = self .moving_mean.to(X.device)self .moving_var = self .moving_var.to(X.device)self .moving_mean, self .moving_var = batch_norm(self .gamma, self .beta, self .moving_mean,self .moving_var, eps=1e-5 , momentum=0.9 return Y
LeNet 使用批量规范化
1 2 3 4 5 6 7 8 9 10 1 , 6 , kernel_size=5 ), BatchNorm(6 , num_dims=4 ), nn.Sigmoid(),2 , stride=2 ),6 , 16 , kernel_size=5 ), BatchNorm(16 , num_dims=4 ), nn.Sigmoid(),2 , stride=2 ), nn.Flatten(),16 *4 *4 , 120 ), BatchNorm(120 , num_dims=2 ), nn.Sigmoid(),120 , 84 ), BatchNorm(84 , num_dims=2 ), nn.Sigmoid(),84 , 10 )
训练
1 2 3 lr, num_epochs, batch_size = 1.0 , 10 , 256
1 2 3 loss 0.267, train acc 0.900, test acc 0.860
简明实现
1 2 3 4 5 6 7 8 9 10 11 1 , 6 , kernel_size=5 ), nn.BatchNorm2d(6 ), nn.Sigmoid(),2 , stride=2 ),6 , 16 , kernel_size=5 ), nn.BatchNorm2d(16 ), nn.Sigmoid(),2 , stride=2 ), nn.Flatten(),256 , 120 ), nn.BatchNorm1d(120 ), nn.Sigmoid(),120 , 84 ), nn.BatchNorm1d(84 ), nn.Sigmoid(),84 , 10 )
再次训练
1 d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
1 2 3 loss 0.263, train acc 0.902, test acc 0.862
争议
实践证明批量规范化是一种有效的方法,但它为什么有效,目前我们还没有找到合适的理论来解释它。
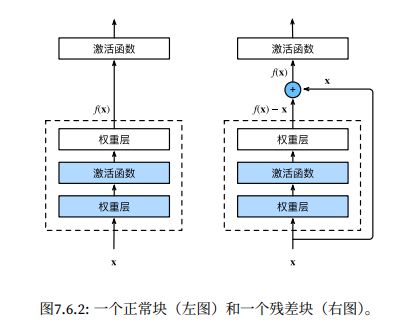
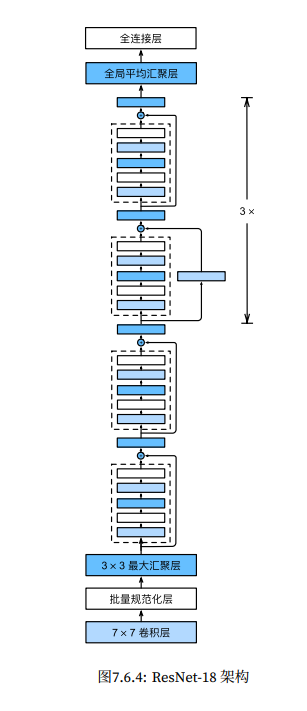
残差网络 ResNet
深度学习的网络层数并不是越多越好,因为实践中发现,随着层数变多,模型性能并不必然变好,甚至还会出现退化。因为随着深度的增加,逐级更新的梯度有可能变得越来小,有可能是因为梯度消失,也有可能是梯度爆炸。最终导致接近输入层的参数,几乎得不到有效的更新,因此模型的性能提升就卡住了。
在残差网络结构出现之前,模型主要的目标是学习映射。残差网络改变了这一个范式,它让模型转向学习映射和输入的残差,这样就巧妙避开了梯度消失的问题,所有的输入都能够得以保留并向后传递。
函数类
深度学习有点像是在一个函数集中,寻找表现最佳的某个子函数。理论上,通过扩大函数集,我们就有可能找到更优解。但事实并非如此,关键在于旧的函数集,必须为新的函数集的子集,即二者需要是嵌套的关系。这样才能保证旧的最优解,仍然包含在新的函数集中。如果不是如此,即使新的函数可能更大,但由于它出现了飘移,有可能离最优解更远了。
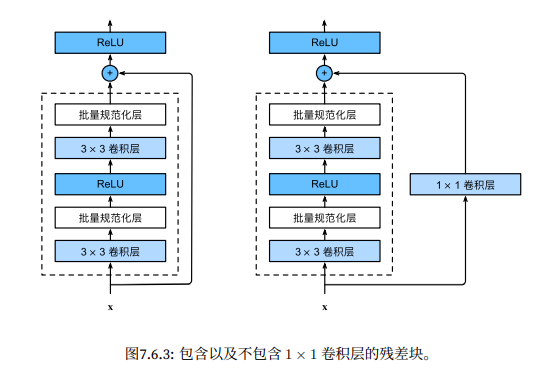
残差块
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import torchfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2lclass Residual (nn.Module):def __init__ (self, input_channels, num_channels, use_1x1conv=False , strides=1 ):super ().__init__()self .conv1 = nn.Conv2d(3 , padding=1 ,strides=stridesself .conv2 = nn.Conv2d(3 , padding=1 if use_1x1conv:self .conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1 , strides=strides)else :self .conv3 = None self .bn1 = nn.BatchNorm2d(num_channels)self .bn2 = nn.BatchNorm2d(num_channels)def forward (self, X ):self .bn1(self .conv1(X)))self .bn2(self .conv2(Y))if self .conv3:self .conv3(X)return F.relu(Y)
1 2 3 4 blk = Residual(3 ,3 )4 , 3 , 6 , 6 )
1 torch.Size([4, 3, 6, 6])
1 2 3 4 5 3 , 6 , use_1x1conv=True , strides=2 )
1 torch.Size([4, 6, 3, 3])
ResNet 模型
ResNet 和 GoogleNet 的区别:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 b1 = nn.Sequential(1 , 64 , kernel_size=7 , stride=2 , padding=3 ),64 ), 3 , stride=2 , padding=1 )def resnet_block (input_channels, num_channels, num_residuals, first_block=False ):for i in range (num_residuals):if i == 0 and not first_block:True , strides=2 ))else :return blk64 , 64 , 2 , first_block=True ))64 , 128 , 2 ))128 , 256 , 2 ))256 , 512 , 2 ))1 , 1 ),512 , 10 )
1 2 3 4 X = torch.rand(size=(1 , 1 , 224 , 224 ))for layer in net:print (layer.__class__.__name__,'output shape:\t' , X.shape)
1 2 3 4 5 6 7 8 Sequential output shape: torch.Size([1, 64, 56, 56])
训练模型
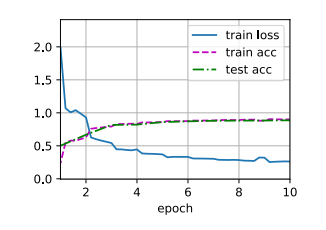
1 2 3 lr, num_epochs, batch_size = 0.05 , 10 , 256 96 )
1 2 3 loss 0.008, train acc 0.999, test acc 0.898
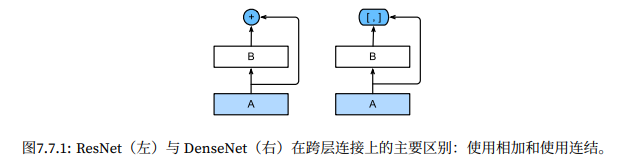
稠密连接网络 DenseNet
从 ResNet 到 DenseNet
泰勒展开式:任意一个可以无限求导的光滑函数,都可以使用一个多项式来近似。
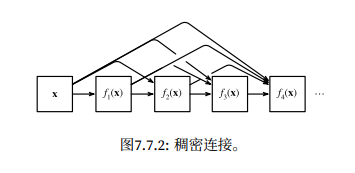
稠密连接:网络中的每一层,都和后面的每一层相关联。它表示第 N 层,会收到前面 [1, 2, 3, …, N - 1] 层的 concat 拼接输出做为输入;这意味着每一层的输入,会随着深度的增加,维数变得越来越多。它的好处如下:
特征高效复用:后面的任意一层,都可以轻易的获得前面任意一层的计算结果,相当于能够读取前面任意一层提取的特征;
避免特征重复:每一层的参数自动倾向于学习新的特征,因为旧特征已经在输入里面了;
计算性能提升:因为减少了重复的特征,因此需要的参数总量反而减少了;
缓解梯度消失;
稠密块体
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 import torchfrom torch import nnfrom d2l import torch as d2ldef conv_block (input_channels, num_channels ):return nn.Sequential(3 , padding=1 )class DenseBlock (nn.Module):def __init__ (self, num_convs, input_channels, num_channels ):super (DenseBlock, self ).__init__()for i in range (num_convs):self .net = nn.Sequential(layers)def forward (self, X ):for blk in self .net:1 )return X
1 2 3 4 blk = DenseBlock(2 , 3 , 10 ) 4 , 3 , 8 , 8 )
1 torch.Size([4, 23, 8, 8])
过渡层
每一个稠密块都会累加输出维度,为了避免输出维数过多,可考虑通过
1 × 1
卷积层来合并通道,减少输出维数;
1 2 3 4 5 6 7 8 9 10 def transition_block (input_channels, num_channels ):return nn.Sequential(1 ), 2 , stride=2 ) 23 , 10 )
1 torch.Size([4, 10, 4, 4])
DenseNet 模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 , 64 , kernel_size=7 , stride=2 , padding=3 ),64 ), nn.ReLU(),3 , stride=2 , padding=1 )64 , 32 4 , 4 , 4 , 4 ] for i, num_convs in enumerate (num_convs_in_dense_blocks):if i != len (num_convs_in_dense_blocks) - 1 :2 ))2 ;1 , 1 )),10 )
训练模型
1 2 3 lr, num_epochs, batch_size = 0.1 , 10 , 256 96 )
1 2 3 loss 0.140, train acc 0.950, test acc 0.882
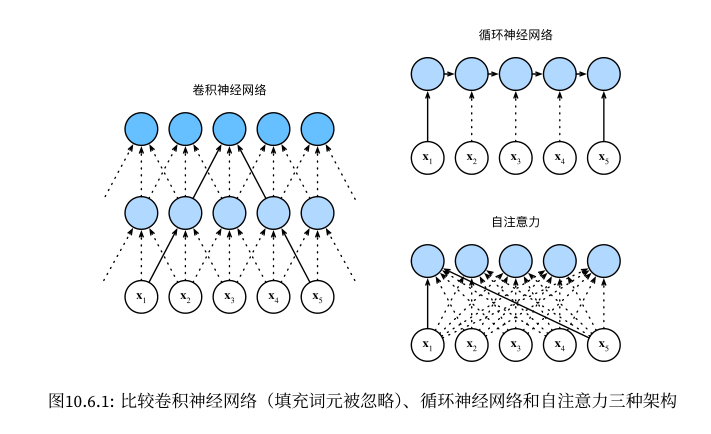
循环神经网络
卷积网络可用于处理空间数据,循环网络则主要用来处理序列的数据,例如文本数据。
序列模型
统计工具
自回归模型
用过去的一段历史数据,预测未来的值,例如预测天气。
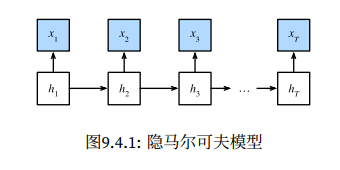
马尔可夫模型
马尔可夫模型背后隐含着一个前提,系统在运行足够长的时间后,其中各种状态的分布概率会稳定下来,称为“稳态分布”;
模型涉及以下几个概念:
状态空间:所有可能的状态的集合;
转移概率:系统从一个状态转移到下一个状态的概率;
转移概率矩阵:系统在不同的状态之间转移切换的概率,可以使用一个矩阵来表示;
稳态分布:系统从长期来看会趋于稳定;
马尔可夫模型有以下几个应用:
自然语言的处理:机器翻译、语音识别等;
预测分析:
网页排序:将网页间的链接看作一种状态转移。通过转移的次数,判断每个网页链接的重要性;
金融风控:例如通过信用卡的使用,预测其未来违约的可能性;
自回归模型有一个变体是隐变量的自回归模型。所谓的隐变量是指驱动状态变化的一些变量,我们无法直接观测,我们只能观察到部分变量。当标准的可充分观测的模型,无法准确描述数据的动力学特性时,我们即需要考虑是否改用包含隐变量的自回归模型。
训练
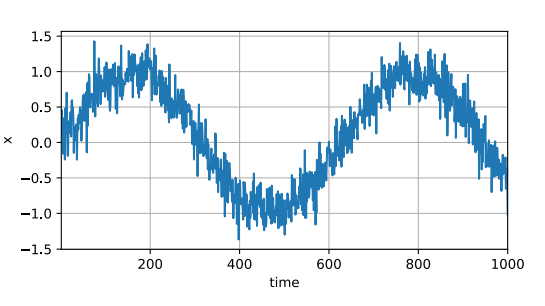
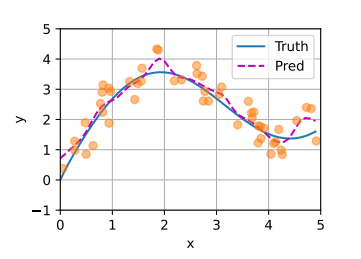
1 2 3 4 5 6 7 8 9 import torchfrom torch import nnfrom d2l import torch as d2l1000 1 , T + 1 , dtype=torch.float32)0.01 * time) + torch.normal(0 , 0.2 , (T,))'time' , 'x' , xlim=[1 , 1000 ], figsize=(6 , 3 ))
1 2 3 4 5 6 4 for i in range (tau):1 , 1 ))
1 2 3 4 batch_size, n_train = 16 , 600 True )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def init_weights (m ):if type (m) == nn.Linear:def get_net ():4 , 10 ),10 , 1 )return net'none' )
1 2 3 4 5 6 7 8 9 10 11 12 13 def train (net, train_iter, loss, epochs, lr ):for epoch in range (epochs):for X, y in train_iter:sum ().backward()print (f'epoch {epoch + 1 } , ' f'loss: {d2l.evaluate_loss(net, train_iter, loss):f} ' )5 , 0.01 )
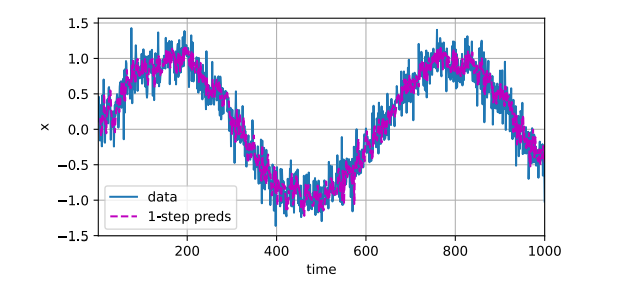
1 2 3 4 5 epoch 1, loss: 0.063133
预测
1 2 3 4 5 6 'time' ,'x' , legend=['data' , '1-step preds' ], xlim=[1 , 1000 ],6 , 3 ))
单步预测的性能不错,但是如果使用模型预测更远期的值,例如尝试预测 14 天后的值,则错误会越来越明显。因为接下来 14 天的值我们都是不知道的。因此每一天都需要使用这个模型预测,直到第 14 天。因为我们的模型不是完美的,每一次预测都在存在微小的误差。在对未来 14 天的预测过程中,这个误差会不断累积。最后导致实际的结果和真实的结果差异很大。这就好比预测 14 天后的天气情况,远不如预测明天的天气来得准确。
文本预处理
文本的预处理一般包括:
将文本加载到内存中;
将文本拆分为词元(单词、符号);
创建一个词汇表,给每个词元一个编号;
将文本中的每个词元,替换成编号;
语言模型和数据集
每个词元相当于一个观测结果。一个词元连接的下一个词元,类似于从一个观测切换到另外一人观测;语言模型需要找到概率最大的下一个观测。
概率大可能满足语法和常用短语的需求,但它出来的结果不一定是最合理的答案,有可能只是最常见的错误答案。
学习语言模型
下一个词元的概率预测公式如下:
P ( x 1 , x 2 , … , x T ) = ∏ t = 1 T P ( x t ∣ x 1 , … , x t − 1 )
例如:
P ( deep , learning , is , fun ) = P ( deep ) P ( learning ∣ deep ) P ( is ∣ deep , learning ) P ( fun ∣ deep , learning , is ) .
马尔可夫模型与 n 元语法
可用于建模的近似公式:
P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ) P ( x 4 ) , P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ∣ x 1 ) P ( x 3 ∣ x 2 ) P ( x 4 ∣ x 3 ) , P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ∣ x 1 ) P ( x 3 ∣ x 1 , x 2 ) P ( x 4 ∣ x 2 , x 3 ) .
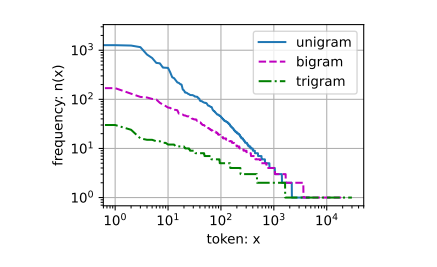
自然语言统计
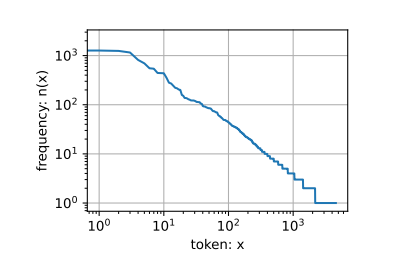
不同单词在句子中出现的频率(即词频)存在非常显著的差异化,总体来说呈对数分布
以下是一元、二元、三元语法各自的词频分布图:
总的来说,它们都遵循类似的分布规律。如果将单词进行任意的组合,那么其中的绝大部分组合是不会出现的。
读取长序列数据
随机采样
任意子序列
同个小批量不必然相邻
标签:移位一个词元的原始序列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 def seq_data_iter_random (corpus, batch_size, num_steps ):"""使用随机抽样生成一个小批量子序列""" 0 , num_steps - 1 )len (corpus) - 1 ) // num_stepslist (range (0 , num_subseqs * num_steps, num_steps))def data (pos ):return corpus[pos: pos + num_steps]for i in range (0 , batch_size * num_batches, batch_size):for j in initial_indices_per_batch]1 ) for j in initial_indices_per_batch]yield torch.tensor(X), torch.tensor(Y)
1 2 3 my_seq = list (range (35 ))for X, Y in seq_data_iter_random(my_seq, batch_size=2 , num_steps=5 ):print ('X: ' , X, '\nY:' , Y)
1 2 3 4 5 6 7 8 9 10 11 12 X: tensor([[26, 27, 28, 29, 30],
顺序分区
小批量内部的子序列不相邻,但相邻小批量的的子序列,可以设置为相邻,实现顺序分区;
1 2 3 4 5 6 7 8 9 10 11 12 13 def seq_data_iter_sequential (corpus, batch_size, num_steps ): """使用顺序分区生成一个小批量子序列""" 0 , num_steps)len (corpus) - offset - 1 ) // batch_size) * batch_size1 : offset + 1 + num_tokens])1 ), Ys.reshape(batch_size, -1 )1 ] // num_stepsfor i in range (0 , num_steps * num_batches, num_steps):yield X, Y
1 2 for X, Y in seq_data_iter_sequential(my_seq, batch_size=2 , num_steps=5 ):print ('X: ' , X, '\nY:' , Y)
1 2 3 4 5 6 7 8 9 10 11 12 X: tensor([[ 2, 3, 4, 5, 6],
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class SeqDataLoader : """加载序列数据的迭代器""" def __init__ (self, batch_size, num_steps, use_random_iter, max_tokens ):if use_random_iter:self .data_iter_fn = d2l.seq_data_iter_randomelse :self .data_iter_fn = d2l.seq_data_iter_sequentialself .corpus, self .vocab = d2l.load_corpus_time_machine(max_tokens)self .batch_size, self .num_steps = batch_size, num_stepsdef __iter__ (self ):return self .data_iter_fn(self .corpus, self .batch_size, self .num_steps)def load_data_time_machine (batch_size, num_steps, use_random_iter=False , max_tokens=10000 ):"""返回时光机器数据集的迭代器和词表""" return data_iter, data_iter.vocab
循环神经网络
使用隐藏变量防止参数数量爆炸
P ( x t ∣ x t − 1 , … , x 1 ) ≈ P ( x t ∣ h t − 1 )
此处使用隐藏变量
h t − 1
来代表当前的隐藏状态,用于存储当前序列之前的历史信息,它的计算方法如下:
h t = f ( x t , h t − 1 )
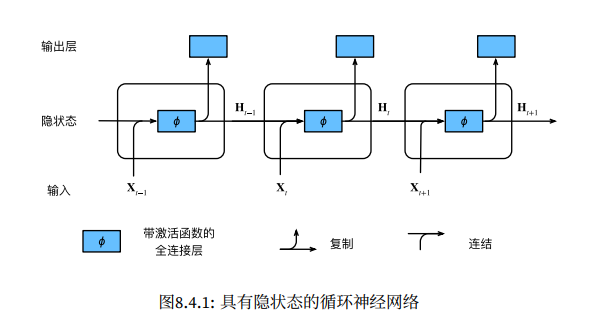
循环神经网络是包含隐藏状态的神经网络。
无隐状态的神经网络
跟多层感知机没什么区别
有隐状态的神经网络
每个样本拥有一个隐藏状态变量,这个变量由当前输入和上一步的隐藏变量*权重参数计算得出。
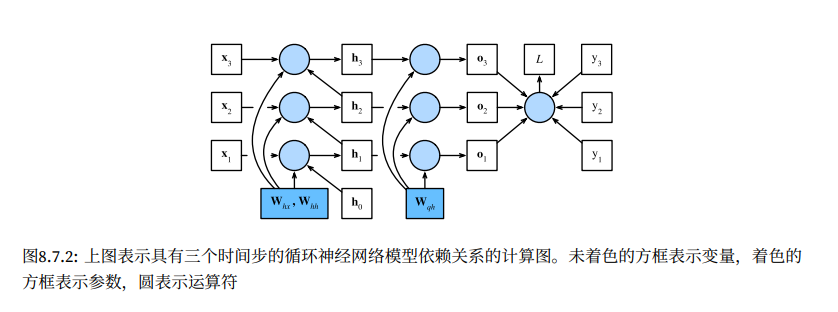
H t = ϕ ( X t W x h + H t − 1 W h h + b h )
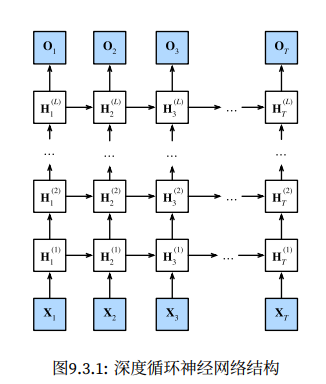
由于每一步的隐状态是基于上一步循环计算出来的,所以该神经网络模型被称为循环神经网络,recurrent neural network,模型中有一个循环层用来计算出上述的隐状态。模型包含以下两种类型的权重参数:
隐藏层的权重
W x h ∈ R d × h , W h h ∈ R h × h
和偏置
b h ∈ R 1 × h
输出层的权重
W h q ∈ R h × q
和偏置
b q ∈ R 1 × q
以下是三个相邻时间步的计算过程示意:
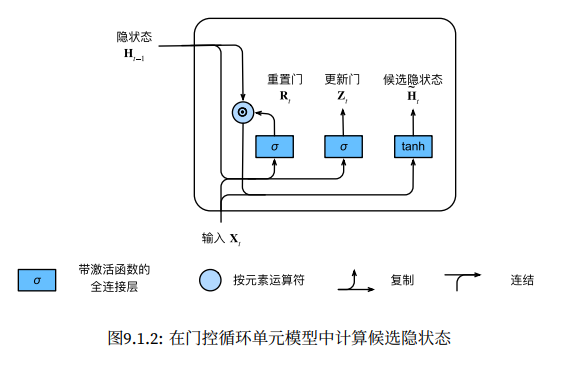
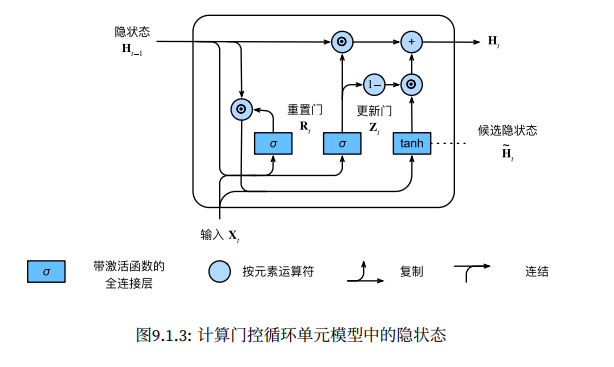
用代码展示计算过程
1 2 3 4 5 6 import torchfrom d2l import torch as d2l0 , 1 , (3 , 1 )), torch.normal(0 , 1 , (1 , 4 ))0 , 1 , (3 , 4 )), torch.normal(0 , 1 , (4 , 4 ))
1 2 3 tensor([[ 0.2321, -0.9882, -1.6137, -1.0731],
1 2 3 1 ), torch.cat((W_xh, W_hh), 0 ))
1 2 3 tensor([[ 0.2321, -0.9882, -1.6137, -1.0731],
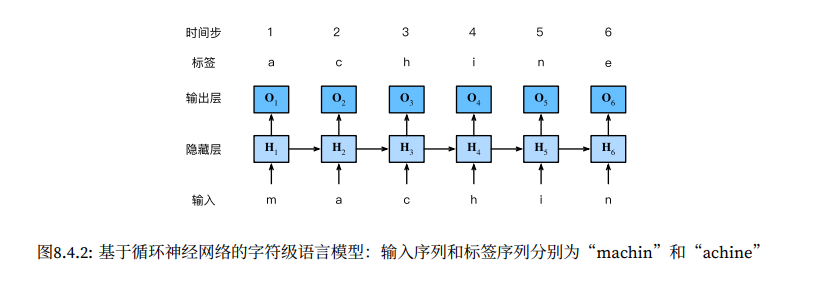
基于循环神经网络的字符级语言模型
困惑度
如何评估模型质量?可以计算序列的似然概率,但貌似容易失真,因为短序列比长序列出现概率更高。信息论出场。
一个更好的模型,允许我们在压缩序列时,使用更少的比特。因此可以用序列中 n 个词元的交叉熵损失来衡量模型质量。
1 n ∑ t = 1 n − log P ( x t ∣ x t − 1 , … , x 1 )
困惑度的公式等同于交叉熵的指数形式:
exp ( − 1 n ∑ t = 1 n log P ( x t ∣ x t − 1 , … , x 1 ) )
困惑度:用来衡量模型的好坏。相当于模型对下一个词元的不确定性。
当估计标签词元的概率为 1 时,模型的困惑度为 1;没有困惑;
当估计标签词元的概率为 0 时,模型的困惑度为无穷大;
循环神经网络从零实现
1 2 3 4 5 6 7 8 import mathimport torchfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2l32 , 35
独热编码
1 2 3 4 5 6 7
定义一个 one_hot 函数,用来将二维的小批量样本,转成三维张量,第三维是独热,维度等同于词表的大小。
1 2 X = torch.arange(10 ).reshape((2 , 5 ))28 ).shape
初始化模型参数
隐藏单元数量,是一个超参数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def get_params (vocab_size, num_hiddens, device ):def normal (shape ):return torch.randn(size=shape, device=device) * 0.01 for param in params:True )return params
循环神经网络模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def init_rnn_state (batch_size, num_hiddens, device ):return (torch.zeros((batch_size, num_hiddens), device=device), )def rnn (inputs, state, params ):for X in inputs:return torch.cat(outputs, dim=0 ), (H,)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class RNNModelScratch : """从零开始实现的循环神经网络模型""" def __init__ (self, vocab_size, num_hiddens, device, get_params, init_state, forward_fn ):self .vocab_size, self .num_hiddens = vocab_size, num_hiddensself .params = get_params(vocab_size, num_hiddens, device)self .init_state, self .forward_fn = init_state, forward_fndef __call__ (self, X, state ):self .vocab_size).type (torch.float32)return self .forward_fn(X, state, self .params)def begin_state (self, batch_size, device ):return self .init_state(batch_size, self .num_hiddens, device)
1 2 3 4 5 6 num_hiddens = 512 len (vocab), num_hiddens, d2l.try_gpu(), get_params, init_rnn_state, rnn)0 ], d2l.try_gpu())len (new_state), new_state[0 ].shape
1 (torch.Size([10, 28]), 1, torch.Size([2, 512]))
预测
在真正的预测前,模型需要先热身,以便更新隐藏状态。预热结束后,才具备预测的条件。
1 2 3 4 5 6 7 8 9 10 11 12 def predict_ch8 (prefix, num_preds, net, vocab, device ): """在prefix后面生成新字符""" 1 , device=device)0 ]]]lambda : torch.tensor([outputs[-1 ]], device=device).reshape((1 , 1 ))for y in prefix[1 :]: for _ in range (num_preds): int (y.argmax(dim=1 ).reshape(1 )))return '' .join([vocab.idx_to_token[i] for i in outputs])
1 predict_ch8('time traveller ' , 10 , net, vocab, d2l.try_gpu())
1 'time traveller omrnya qmg'
梯度裁剪
假设有 T 个时间步,那么在反向传播更新梯度时,乘法链的长度为
O ( T )
,随着 T 变大,可能会出现梯度消失或爆炸。
如何保证训练的稳定性?其中一种方法是“梯度裁剪”,它可以用来避免梯度爆炸。
核心思想:设定一个阈值,如果梯度向量的范数超过这个阈值,就将梯度按比例缩小,让范数刚好等于阈值。
1 2 3 4 5 6 7 8 9 10 """裁剪梯度""" def grad_clipping (net, theta ):if isinstance (net, nn.Module):for p in net.parameters() if p.requires_grad]else :sum (torch.sum ((p.grad ** 2 )) for p in params))if norm > theta:for param in params:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 """训练网络一个迭代周期""" def train_epoch_ch8 (net, train_iter, loss, updater, device, use_random_iter ):None , d2l.Timer()2 ) for X, Y in train_iter:if state is None or use_random_iter:0 ], device=device)else :if isinstance (net, nn.Module) and not isinstance (state, tuple ):else :for s in state:1 )if isinstance (updater, torch.optim.Optimizer):1 ) else :1 )1 )return math.exp(metric[0 ] / metric[1 ]), metric[1 ] / timer.stop()
之所以要分离梯度,是因为隐状态是循环计算得来的,因此它涉及同一个训练周期中,所以小批量数据,这会导致计算的复杂度爆炸。因此,通过临时梯度分离,让隐状态的梯度更新,局限在当前小批量的时间步内。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 """训练模型""" def train_ch8 (net, train_iter, vocab, lr, num_epochs, device, use_random_iter=False ):'epoch' , ylabel='perplexity' ,'train' ], xlim=[10 , num_epochs])if isinstance (net, nn.Module):else :lambda batch_size: d2l.sgd(net.params, lr, batch_size)lambda prefix: predict_ch8(prefix, 50 , net, vocab, device)for epoch in range (num_epochs):if (epoch + 1 ) % 10 == 0 :print (predict('time traveller' ))1 , [ppl])print (f'困惑度 {ppl:.1 f} , {speed:.1 f} 词元/秒 {str (device)} ' )print (predict('time traveller' ))print (predict('traveller' ))
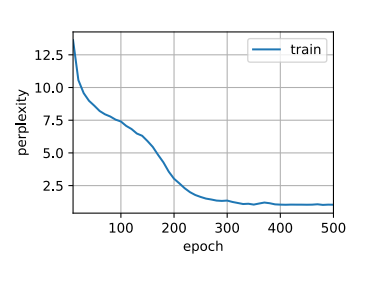
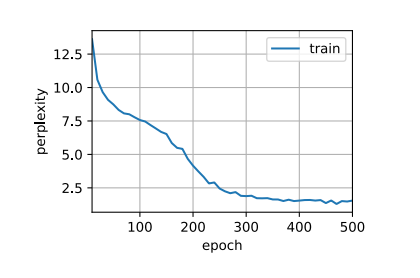
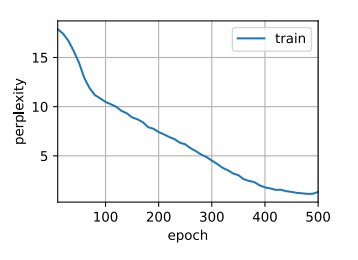
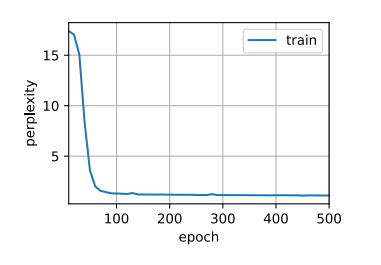
1 2 num_epochs, lr = 500 , 1
1 2 3 困惑度 1.0, 12401.8 词元/秒 cpufor so it will be convenient to speak of himwas e
1 2 3 4 net = RNNModelScratch(len (vocab), num_hiddens, d2l.try_gpu(), get_params,True )
1 2 3 困惑度 1.4, 70725.7 词元/秒 cuda:0fi fi
循环神经网络的简洁实现
1 2 3 4 5 6 7 import torchfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2l32 , 35
1 2 num_hiddens = 256 len (vocab), num_hiddens)
1 2 state = torch.zeros((1 , batch_size, num_hiddens))
1 torch.Size([1, 32, 256])
1 2 3 X = torch.rand(size=(num_steps, batch_size, len (vocab)))
1 (torch.Size([35, 32, 256]), torch.Size([1, 32, 256]))
定义循环神经网络模型
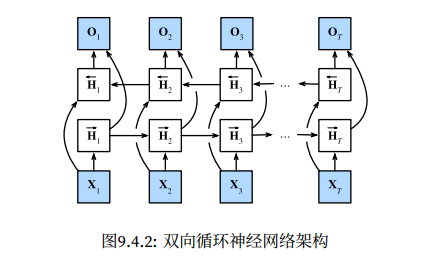
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 """循环神经网络模型""" class RNNModel (nn.Module):def __init__ (self, rnn_layer, vocab_size, **kwargs ):super (RNNModel, self ).__init__(**kwargs)self .rnn = rnn_layerself .vocab_size = vocab_sizeself .num_hiddens = self .rnn.hidden_sizeif not self .rnn.bidirectional:self .num_directions = 1 self .linear = nn.Linear(self .num_hiddens, self .vocab_size)else :self .num_directions = 2 self .linear = nn.Linear(self .num_hiddens * 2 , self .vocab_size)def forward (self, inputs, state ):self .vocab_size)self .rnn(X, state)self .linear(Y.reshape((-1 , Y.shape[-1 ])))return output, statedef begin_state (self, device, batch_size=1 ):if not isinstance (self .rnn, nn.LSTM):return torch.zeros((self .num_directions * self .rnn.num_layers,self .num_hiddens),else :return (torch.zeros((self .num_directions * self .rnn.num_layers,self .num_hiddens), device=device),self .num_directions * self .rnn.num_layers,self .num_hiddens), device=device))
训练与预测
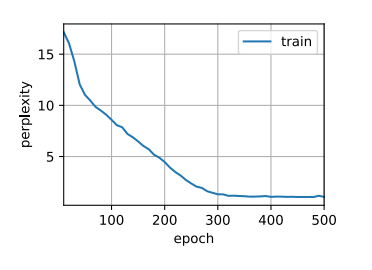
1 2 3 4 5 device = d2l.try_gpu()len (vocab))'time traveller' , 10 , net, vocab, device)
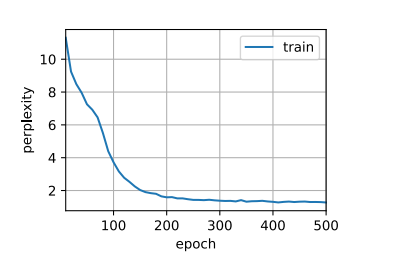
1 2 num_epochs, lr = 500 , 1
1 2 3 perplexity 1.3, 404413.8 tokens/sec on cuda:0for the historia
通过时间反向传播
循环神经网络的梯度分析
由于由于多个时间步的之间的循环计算,因此直接求梯度的话,需要处理这个循环,进行递归计算。当步数较多时,容易出现蝴蝶效应,导致梯度爆炸。初始条件的微小差异,通过递归循环放大了,导致不利于模型的稳定收敛。
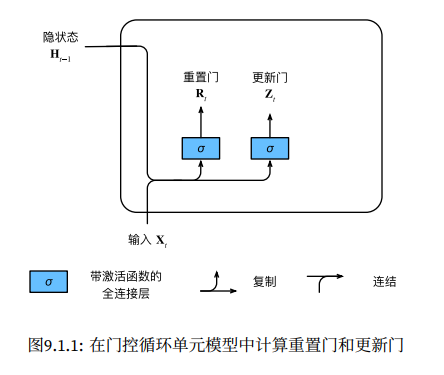
有几种解决办法:
规则截断:在一定的步数后,中止递归,这样会导致模型只关注短期影响,跟现实大致相符,所以效果还可以。
随机截断:
通过时间反向传播的细节
计算目标函数相对所有模型的梯度,假设没有偏置参数,以简化计算过程;激活函数使用恒等映射
现代循环神经网络
门控循环单元
英文:Gate Recurrent Unit,GRU
循环神经网络因为计算链接过长,容易出现梯度消失或爆炸问题。门控机制有点像是引入一个阀门,有选择性的开启或关闭某些计算环节,以过滤不需要的信息,解决梯度消失问题。
存在的问题:
早期的观测值很重要,会影响所有未来的观测,需要有一个机制能够存储早期信息;
存在一些无关紧要的内容,需要忽略;
序列的不同部分可能没有关系;
解决方案:
长短期记忆;
门控机制:引入可训练学习的新机制,用于判断是否更新或重置隐藏状态;
门控隐状态
重置门和更新门
重置门
R t
和更新门
Z t
的计算公式如下:
R t = σ ( X t W x r + H t − 1 W h r + b r ) , Z t = σ ( X t W x z + H t − 1 W h z + b z ) ,
其中
σ
表示这是一个全连接层;即用全连接的方式,来计算重置门和更新门;这里的核心是计算这两个门的权重参数。通过训练找到合适的参数值;
候选隐状态
将重置门应用到隐状态的更新过程中,计算一个候选的隐状态:
H ~ t = tanh ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h )
此处使用 tanh 激活函数,来将计算结果压缩到 [-1, 1] 的区间。
R t ⊙ H t − 1
可用于控制过往状态的影响;
当重置门的值接近 0 时,候选隐状态的值接近于以
X t
作为输入,使用多层感知机计算出来的结果;
当重置门的值接近 1 时,候选隐状态的值接近于常规的循环神经网络计算出来的结果;
隐状态
更新门
Z t
的作用是新的隐状态
H t
有多少比例来自于上一步的隐状态
H t − 1
,有多少比例来自于候选隐状态 ,更新门的计算公式如下:
H t = Z t ⊙ H t − 1 + ( 1 − Z t ) ⊙ H ~ t .
当更新门的值接近 0 时,新的隐状态更接近候选状态
H ~ t
的值;
当更新门的值接近 1 时,新的隐状态更接近旧的隐状态
H t − 1
的值,相当于保留旧状态,跳过当前输入
X t
带来的影响;
更新门因为可跳过当前输入的影响,因此它可用于捕捉长期依赖关系;
重置门因为可以忽略过往的信息,只保留当前的信息,因此它可用于捕捉短期依赖关系;
从零开始实现
初始化模型参数
1 2 3 4 5 6 import torchfrom torch import nnfrom d2l import torch as d2l32 , 35
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def get_params (vocab_size, num_hiddens, device ):def normal (shape ):return torch.randn(size=shape, device=device)*0.01 def three ():return (normal((num_inputs, num_hiddens)),for param in params:True )return params
定义模型
1 2 3 def init_gru_state (batch_size, num_hiddens, device ):return (torch.zeros((batch_size, num_hiddens), device=device), )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 def gru (inputs, state, params ):for X in inputs:1 - Z) * H_tildareturn torch.cat(outputs, dim=0 ), (H,)
训练与预测
1 2 3 4 5 vocab_size, num_hiddens, device = len (vocab), 256 , d2l.try_gpu()500 , 1 len (vocab), num_hiddens, device, get_params,
1 2 3 perplexity 1.3, 28030.1 tokens/sec on cuda:0
简洁实现
1 2 3 4 5 num_inputs = vocab_sizelen (vocab))
1 2 3 perplexity 1.1, 334788.1 tokens/sec on cuda:0
长短期记忆网络
英文:Long-Short Term Memory,LSTM
LSTM 想要解决的问题和 GRU 一样,即循环模型常见的长期信息记忆和短期输入缺失的问题。它的解决䢍比 GRU 稍微复杂一些,但它却出现得更早,早了近 20 年。
LSTM 和 GRU 的区别在于,它除了隐状态,还多了一个记忆元;
门控记忆元
LSTM 的设计灵感来源于计算机的逻辑门设计。
输入门、输出门、遗忘门
输入门是
I t ∈ R n × h
,遗忘门是
F t ∈ R n × h
,输出门是
O t ∈ R n × h
。三者的计算公式如下:
I t = σ ( X t W x i + H t − 1 W h i + b i ) , F t = σ ( X t W x f + H t − 1 W h f + b f ) , O t = σ ( X t W x o + H t − 1 W h o + b o ) ,
三者的作用如下:
记忆元:也叫细胞,是信息记忆的载体,通过遗忘门和输入门进行更新;
输入门:决定从当前的输入中,读取多少新信息到记忆元中;
遗忘门:决于过往的记忆元中要遗忘哪些信息;
输出门:决定当前的记忆元中需要输出哪些信息作为新的隐状态;
候选记忆元
候选记忆元
C ~ t
计算公式同以上三个门相同,差别在于使用 tanh 做为激活函数
C ~ t = tanh ( X t W x c + H t − 1 W h c + b c )
记忆元
对于记忆元中
C t
的数据,输入门
I t
用来控制采纳多少新数据
C ~ t
,遗忘门
F t
用来控制采纳多少旧数据
C t − 1
C t = F t ⊙ C t − 1 + I t ⊙ C ~ t
在 GRU 中,输入门和遗忘门貌似合并成了一个,即更新门;
隐状态
隐状态
H t
是输出门
O t
和 tanh 版本的记忆元
C t
的计算结果,计算公式如下:
H t = O t ⊙ tanh ( C t )
当输出门接近 1 时,相当于传递当前输入的信息;
当输出门接近 0 时,相当于忽略当前输入的信息;
从零开始实现
初始化模型参数
1 2 3 4 5 6 import torchfrom torch import nnfrom d2l import torch as d2l32 , 35
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def get_lstm_params (vocab_size, num_hiddens, device ):def normal (shape ):return torch.randn(size=shape, device=device)*0.01 def three ():return (normal((num_inputs, num_hiddens)),for param in params:True )return params
定义模型
1 2 3 4 def init_lstm_state (batch_size, num_hiddens, device ):return (torch.zeros((batch_size, num_hiddens), device=device),
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def lstm (inputs, state, params ):for X in inputs:return torch.cat(outputs, dim=0 ), (H, C)
训练和预测
1 2 3 4 5 vocab_size, num_hiddens, device = len (vocab), 256 , d2l.try_gpu()500 , 1 len (vocab), num_hiddens, device, get_lstm_params,
1 2 3 perplexity 1.4, 22462.5 tokens/sec on cuda:0for the brow henint it aneles a overrecured aback
简洁实现
1 2 3 4 5 num_inputs = vocab_sizelen (vocab))
1 2 3 perplexity 1.1, 330289.2 tokens/sec on cuda:0
深度循环神经网络
每个隐藏层既向下一层传递输出,也向下一步的隐藏层传递输出。
函数依赖关系
隐状态的计算公式:
H t ( l ) = ϕ l ( H t ( l − 1 ) W x h ( l ) + H t − 1 ( l ) W h h ( l ) + b h ( l ) )
输出层基于最后一个隐状态:
O t = H t ( L ) W h q + b q ,
使用多少个隐藏层,多少个隐藏单元,需要反复实验才知道,属于模型的超参数。
简洁实现
1 2 3 4 5 6 import torchfrom torch import nnfrom d2l import torch as d2l32 , 35
1 2 3 4 5 6 7 len (vocab), 256 , 2 len (vocab))
训练和预测
1 2 num_epochs, lr = 500 , 2 1.0 , num_epochs, device)
1 2 3 perplexity 1.0, 224250.2 tokens/sec on cuda:0
据说深度循环模型需要大量的调参以便实现收敛,参数初始化也需要小心,不知它的性能表现如何?从困惑度来看,好像是有降低了。
双向循环神经网络
预测下一个输出是一种场景,但不是唯一的场景。例如预测之前的输出,类似完形填空,也是一种场景。针对这种场景,之前的单向模型就不够用了,需要单独建模。
隐马尔可夫模型中的动态规划
动态规划的思路,是基于当前信息,判断最优的下一步信息。这个思路可用于双向开模中,通过后向递归,来求解前面的值;
双向模型
只需要添加一个新的隐藏层,用来反向传递信息,我们即可得到一个双向模型。相当于现在有两个隐状态了,一个是前向状态,一个是新增的反向状态。它们分别有各自的权重参数。
H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) , H ← t = ϕ ( X t W x h ( b ) + H ← t + 1 W h h ( b ) + b h ( b ) ) ,
最后的输出:
O t = H t W h q + b q .
模型的计算代价及其应用
由于有正向+反向,因此梯度求解的链条很长,这导致计算速度比较慢。双向模型在实践中非常少用,使用场景不多。
双向模型的错误应用
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import torchfrom torch import nnfrom d2l import torch as d2l32 , 35 , d2l.try_gpu()len (vocab), 256 , 2 True )len (vocab))500 , 1
困惑度看起来挺好,但实际效果。。。
1 2 3 perplexity 1.1, 109857.9 tokens/sec on cuda:0
双向模型不适合用来单向预测未来,因为每个时间步的隐状态是由前后数据共同决定的,所以更适合给定双向上下文的场景,类似完型填空
机器翻译与数据集
机器翻译是序列模型的一个典型应用场景,它刚好符合将一个输入序列转换成另外一个序列的典型场景。
机器翻译的学习是端到端的,训练数据由包含输入语言和目标语言的文本序列对组成
下载和预处理数据
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import osimport torchfrom d2l import torch as d2l'fra-eng' ] = (d2l.DATA_URL + 'fra-eng.zip' ,'94646ad1522d915e7b0f9296181140edcf86a4f5' )def read_data_nmt ():"""载入“英语-法语”数据集""" 'fra-eng' )with open (os.path.join(data_dir, 'fra.txt' ), 'r' ,'utf-8' ) as f:return f.read()print (raw_text[:75 ])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def preprocess_nmt (text ):"""预处理“英语-法语”数据集""" def no_space (char, prev_char ):return char in set (',.!?' ) and prev_char != ' ' '\u202f' , ' ' ).replace('\xa0' , ' ' ).lower()' ' + char if i > 0 and no_space(char, text[i - 1 ]) else charfor i, char in enumerate (text)]return '' .join(out)print (text[:80 ])
1 2 3 4 5 6 go . va !who ? qui ?
词元化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 def tokenize_nmt (text, num_examples=None ):"""词元化“英语-法语”数据数据集""" for i, line in enumerate (text.split('\n' )):if num_examples and i > num_examples:break '\t' )if len (parts) == 2 :0 ].split(' ' ))1 ].split(' ' ))return source, target6 ], target[:6 ]
1 2 3 4 5 6 7 8 9 10 11 12 ([['go' , '.' ],'hi' , '.' ],'run' , '!' ],'run' , '!' ],'who' , '?' ],'wow' , '!' ]],'va' , '!' ],'salut' , '!' ],'cours' , '!' ],'courez' , '!' ],'qui' , '?' ],'ça' , 'alors' , '!' ]])
1 2 3 4 5 6 7 8 9 10 11 12 13 def show_list_len_pair_hist (legend, xlabel, ylabel, xlist, ylist ):"""绘制列表长度对的直方图""" len (l) for l in xlist], [len (l) for l in ylist]])for patch in patches[1 ].patches:'/' )'source' , 'target' ], '# tokens per sequence' ,'count' , source, target);
可见绝大部分句子的长度小于 20
词表
一些处理方法:
出现频率低的单词,用特殊符号替代,不然词表会很大;
使用填充符号,让序列保持一定的长度;
使用特定符号标注序列的开始和结束;
1 2 3 src_vocab = d2l.Vocab(source, min_freq=2 ,'<pad>' , '<bos>' , '<eos>' ])len (src_vocab)
加载数据集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def truncate_pad (line, num_steps, padding_token ):"""截断或填充文本序列""" if len (line) > num_steps:return line[:num_steps] return line + [padding_token] * (num_steps - len (line)) 0 ]], 10 , src_vocab['<pad>' ])def build_array_nmt (lines, vocab, num_steps ):"""将机器翻译的文本序列转换成小批量""" for l in lines]'<eos>' ]] for l in lines]'<pad>' ]) for l in lines])'<pad>' ]).type (torch.int32).sum (1 )return array, valid_len
训练模型
1 2 3 4 5 6 7 8 9 10 11 12 13 def load_data_nmt (batch_size, num_steps, num_examples=600 ):"""返回翻译数据集的迭代器和词表""" 2 ,'<pad>' , '<bos>' , '<eos>' ])2 ,'<pad>' , '<bos>' , '<eos>' ])return data_iter, src_vocab, tgt_vocab
1 2 3 4 5 6 7 train_iter, src_vocab, tgt_vocab = load_data_nmt(batch_size=2 , num_steps=8 )for X, X_valid_len, Y, Y_valid_len in train_iter:print ('X:' , X.type (torch.int32))print ('X的有效长度:' , X_valid_len)print ('Y:' , Y.type (torch.int32))print ('Y的有效长度:' , Y_valid_len)break
1 2 3 4 5 6 X: tensor([[ 6, 143, 4, 3, 1, 1, 1, 1],
编码器-解码器架构
引入一个高维空间(固定形状的隐状态),用于代表真实语义,作为输入和输出的中介。
编码器
1 2 3 4 5 6 7 8 9 from torch import nnclass Encoder (nn.Module):"""编码器-解码器架构的基本编码器接口""" def __init__ (self, **kwargs ):super (Encoder, self ).__init__(**kwargs)def forward (self, X, *args ):raise NotImplementedError
解码器
1 2 3 4 5 6 7 8 9 10 class Decoder (nn.Module):"""编码器-解码器架构的基本解码器接口""" def __init__ (self, **kwargs ):super (Decoder, self ).__init__(**kwargs)def init_state (self, enc_outputs, *args ):raise NotImplementedErrordef forward (self, X, state ):raise NotImplementedError
合并编码器和解码器
1 2 3 4 5 6 7 8 9 10 11 class EncoderDecoder (nn.Module):"""编码器-解码器架构的基类""" def __init__ (self, encoder, decoder, **kwargs ):super (EncoderDecoder, self ).__init__(**kwargs)self .encoder = encoderself .decoder = decoderdef forward (self, enc_X, dec_X, *args ):self .encoder(enc_X, *args)self .decoder.init_state(enc_outputs, *args)return self .decoder(dec_X, dec_state)
序列到序列学习
全部输入 + 已知输出 -> 全部输出
使用特定符号 表示输出序列的开始; 表示输出序列的结束;
编码器
1 2 3 4 5 import collectionsimport mathimport torchfrom torch import nnfrom d2l import torch as d2l
此处使用循环神经网络,一步一步的生成多个隐状态:
h t = f ( x t , h t − 1 ) .
将多个隐状态转成上下文变量
c = q ( h 1 , … , h T )
使用一个嵌入层,来表示输入词元的特征向量。嵌入层的行数等于词表的大小,列数等于特征向量的维数(一个单词可能有多种意思和使用场景,因此需要多维的特征向量来表示多种场景);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 """用于序列到序列学习的循环神经网络编码器""" class Seq2SeqEncoder (d2l.Encoder):""" vocab_size 词表大小 embed_size 嵌入的维度,相当于单词的特征向量,它会影响能够容纳的单词语义信息 num_hiddens 隐状态的维度,决定能够存储多少上下文状态,用于学习更多的特征 num_layers 隐藏层的数量,决定了模型的深度,用于学习更复杂的序列模式 """ def __init__ (self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0 , **kwargs ):super (Seq2SeqEncoder, self ).__init__(**kwargs)self .embedding = nn.Embedding(vocab_size, embed_size)self .rnn = nn.GRU(embed_size, num_hiddens, num_layers,def forward (self, X, *args ):self .embedding(X)1 , 0 , 2 ) self .rnn(X)return output, state
1 2 3 4 5 6 encoder = Seq2SeqEncoder(vocab_size=10 , embed_size=8 , num_hiddens=16 ,2 )eval ()4 , 7 ), dtype=torch.long)
解码器
当前步隐状态的计算公式:
s t ′ = g ( y t ′ − 1 , c , s t ′ − 1 ) .
上一步的输出
y t ′ − 1
上下文变量
c
上一步隐状态
s t ′ − 1
当前步隐状态
s t ′
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Seq2SeqDecoder (d2l.Decoder):"""用于序列到序列学习的循环神经网络解码器""" def __init__ (self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0 , **kwargs ):super (Seq2SeqDecoder, self ).__init__(**kwargs)self .embedding = nn.Embedding(vocab_size, embed_size)self .rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,self .dense = nn.Linear(num_hiddens, vocab_size)def init_state (self, enc_outputs, *args ):return enc_outputs[1 ]def forward (self, X, state ):self .embedding(X).permute(1 , 0 , 2 )1 ].repeat(X.shape[0 ], 1 , 1 )2 )self .rnn(X_and_context, state)self .dense(output).permute(1 , 0 , 2 )return output, state
1 2 3 4 5 6 7 10 , embed_size=8 , num_hiddens=16 ,2 )eval ()
1 (torch.Size([4, 7, 10]), torch.Size([2, 4, 16]))
损失函数
填充词元的预测不应纳入损失函数的计算范围。可使用 mask 对填充项清零。
1 2 3 4 5 6 7 8 9 10 def sequence_mask (X, valid_len, value=0 ):"""在序列中屏蔽不相关的项""" 1 )None , :] < valid_len[:, None ]return X1 , 2 , 3 ], [4 , 5 , 6 ]])1 , 2 ]))
1 2 tensor([[1, 0, 0],
修改 softmax 交叉熵计算函数,以便忽略不相关的填充项。
1 2 3 4 5 6 7 8 9 10 11 12 13 """带遮蔽的softmax交叉熵损失函数""" class MaskedSoftmaxCELoss (nn.CrossEntropyLoss):def forward (self, pred, label, valid_len ):self .reduction='none' super (MaskedSoftmaxCELoss, self ).forward(0 , 2 , 1 ), label)1 )return weighted_loss
1 2 3 loss = MaskedSoftmaxCELoss()3 , 4 , 10 ), torch.ones((3 , 4 ), dtype=torch.long),4 , 2 , 0 ]))
1 tensor([2.3026, 1.1513, 0.0000])
训练
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 def train_seq2seq (net, data_iter, lr, num_epochs, tgt_vocab, device ):"""训练序列到序列模型""" def xavier_init_weights (m ):if type (m) == nn.Linear:if type (m) == nn.GRU:for param in m._flat_weights_names:if "weight" in param:'epoch' , ylabel='loss' ,10 , num_epochs])for epoch in range (num_epochs):2 ) for batch in data_iter:for x in batch]'<bos>' ]] * Y.shape[0 ],1 , 1 )1 ]], 1 ) sum ().backward() 1 )sum ()with torch.no_grad():sum (), num_tokens)if (epoch + 1 ) % 10 == 0 :1 , (metric[0 ] / metric[1 ],))print (f'loss {metric[0 ] / metric[1 ]:.3 f} , {metric[1 ] / timer.stop():.1 f} ' f'tokens/sec on {str (device)} ' )
1 2 3 4 5 6 7 8 9 10 11 embed_size, num_hiddens, num_layers, dropout = 32 , 32 , 2 , 0.1 64 , 10 0.005 , 300 , d2l.try_gpu()len (src_vocab), embed_size, num_hiddens, num_layers,len (tgt_vocab), embed_size, num_hiddens, num_layers,
1 loss 0.019, 11451.2 tokens/sec on cuda:0
预测
预测时,初始词元是特定符号 ,之后解码器当前步的输入来自于上一个时间步的预测输出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def predict_seq2seq (net, src_sentence, src_vocab, tgt_vocab, num_steps, device, save_attention_weights=False ):"""序列到序列模型的预测""" eval ()' ' )] + ['<eos>' ]]len (src_tokens)], device=device)'<pad>' ])0 )'<bos>' ]], dtype=torch.long, device=device), dim=0 )for _ in range (num_steps):2 )0 ).type (torch.int32).item()if save_attention_weights:if pred == tgt_vocab['<eos>' ]:break return ' ' .join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq
预测序列的评估
BELU 评估法,它最早用于评估机器翻译的质量,核心思想是机器翻译与人类翻译越相似,那么翻译质量越高。它使用 n-gram 精度(貌似也叫 n 元语法,n 一般取值 1~4)来计算相似性。另外还有一个长度惩罚机制,避免过短的翻译获得高分。
n-gram 精度:计算机器翻译的结果中,n-gram 出现的次数在参数译文中出现的次数,求和后除以机器翻译中总的 n-gram 次数;
n 分别取值 1-4,最后则加权求平均(权重都为 1/4)
BLEU = B P × exp ( ∑ n = 1 N w n log p n )
其中:
-
p n
是修改后的 n-gram 精度,通过 log 将连乘转成了求和
-
w n
= 1/N (通常 N=4)
- BP 是 brevity penalty(长度惩罚)
长度惩罚
B P = { 1 if c > r exp ( 1 − r / c ) if c ≤ r
其中:
- ( c ) 是候选译文的总长度(词数)
- ( r ) 是参考译文的有效长度 (通常取与候选长度最接近的参考译文长度,或所有参考的最短/平均长度)
优点:计算高效,结果有相关性,因此使用广泛;
缺点:与词序无关、不能分辨同义词、单句翻译质量不好;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 """计算BLEU""" def bleu (pred_seq, label_seq, k ): ' ' ), label_seq.split(' ' )len (pred_tokens), len (label_tokens)min (0 , 1 - len_label / len_pred))for n in range (1 , k + 1 ):0 , collections.defaultdict(int )for i in range (len_label - n + 1 ):' ' .join(label_tokens[i: i + n])] += 1 for i in range (len_pred - n + 1 ):if label_subs[' ' .join(pred_tokens[i: i + n])] > 0 :1 ' ' .join(pred_tokens[i: i + n])] -= 1 pow (num_matches / (len_pred - n + 1 ), math.pow (0.5 , n))return score
1 2 3 4 5 6 7 'go .' , "i lost ." , 'he\'s calm .' , 'i\'m home .' ]'va !' , 'j\'ai perdu .' , 'il est calme .' , 'je suis chez moi .' ]for eng, fra in zip (engs, fras):print (f'{eng} => {translation} , bleu {bleu(translation, fra, k=2 ):.3 f} ' )
1 2 3 4 go . => va !, bleu 1.000'ai perdu ., bleu 1.000 he' s calm . => il est bon ?, bleu 0.537'm home . => je suis chez moi debout ., bleu 0.803
在编码器-解码器的架构中,使用了两个循环模型,一个用于编码,一个用于解码。
束搜索
贪心搜索
在每一个 step 中,从所有候选词中,选择概率最大的那个,直到出现最后一个候选词出现结束符 时停止。
但是这个算法有一个问题,由于当前的概率分布,跟过往的选择有关。过往的局部最大概率,并不代表全局最大概率。因此,当步数一多,我们很难知道全局的最大概率是什么。
穷举搜索
穷举搜索就如其名字一般,穷举所有可能性,从中选择概率最大的那个。这个算法虽然可以保证全局最优,但是计算成本比较大。计算代价是
O ( | Y | T ′ )
. 当 step 值较大时,代价指数级上升。
束搜索
束搜索是贪心搜索的改进版本,每个 step 它不再只是选择概率最高的那一个,而是选择概率最高的前几个。然后根据最后的组合,选择概率最大的那个。束搜索有点像是综合了穷举和贪心两个算法的优点,取一个折中
注意力机制
注意力提示
生物学中的注意力提示
非自主性提示:物体在环境中的突出性和易见性。
自主性提示:大脑有意识的选择想要关注的物体。
查询、键、值
我们可尝试对注意力进行建模。最大池化或者平均池化,有点类似非自主性提示。查询则有点类似自主性提示。
输入感官的是数据,这些数据可以用"值"来表示。
"键"有点类似我们对世界的分类抽象,用不同的键,代表不同的事物。
我们可使用注意力池化方法,筛选出特定的"键",以代表我们想要关注的事物。然后再用筛选结果与"值"进行聚合,计算得到想要的输出。
注意力的可视化
使用热力图可视化注意力权重参数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import torchfrom d2l import torch as d2ldef show_heatmaps (matrices, xlabel, ylabel, titles=None , figsize=(2.5 , 2.5 cmap='Reds' ):"""显示矩阵热图""" 0 ], matrices.shape[1 ]True , sharey=True , squeeze=False )for i, (row_axes, row_matrices) in enumerate (zip (axes, matrices)):for j, (ax, matrix) in enumerate (zip (row_axes, row_matrices)):if i == num_rows - 1 :if j == 0 :if titles:0.6 );
1 2 attention_weights = torch.eye(10 ).reshape((1 , 1 , 10 , 10 ))'Keys' , ylabel='Queries' )
1 2 3 4 5 6 7 8 9 10 11
注意力汇聚
生成数据集
使用以下公式生成训练用的数据集
y i = 2 sin ( x i ) + x i 0.8 + ϵ
1 2 3 4 5 6 7 8 9 10 n_train = 50 5 ) def f (x ):return 2 * torch.sin(x) + x**0.8 0.0 , 0.5 , (n_train,)) 0 , 5 , 0.1 ) len (x_test)
1 2 3 4 def plot_kernel_reg (y_hat ):'x' , 'y' , legend=['Truth' , 'Pred' ],0 , 5 ], ylim=[-1 , 5 ])'o' , alpha=0.5 );
平均汇聚
计算样本的平均值
f ( x ) = 1 n ∑ i = 1 n y i
1 2 3 y_hat = torch.repeat_interleave(y_train.mean(), n_test)
非参数注意力汇聚
根据输入的位置,对输出
y i
进行加权求和,而不是平均加权
f ( x ) = ∑ i = 1 n α ( x , x i ) y i
其中
x
是查询,
( x , x i )
是键值对,
α ( x , x i )
计算不同的注意力权重。
注意力权重可以有多种不同的计算方法,例如可以按距离。如是一个键
x i
越靠近查询
x
,则权重越大,相当于获得了更多的注意力。
f ( x ) = ∑ i = 1 n α ( x , x i ) y i = ∑ i = 1 n softmax ( − 1 2 ( x − x i ) 2 ) y i .
这种按距离的权重计算方法不包含可训练的参数,是一种写死的算法。虽然预测的准确率有限,但比简单的加权平均进步了一些。
1 2 3 4 5 6 7 8 9 1 , n_train))2 / 2 , dim=1 )
1 2 3 4 0 ).unsqueeze(0 ),'Sorted training inputs' ,'Sorted testing inputs' )
带参数注意力汇聚
添加一个可学习的参数
w
f ( x ) = ∑ i = 1 n α ( x , x i ) y i = ∑ i = 1 n softmax ( − 1 2 ( ( x − x i ) w ) 2 ) y i .
批量矩阵乘法
1 2 3 4 X = torch.ones((2 , 1 , 4 ))2 , 4 , 6 ))
可使用以上批量矩阵乘法来计算加权平均值
1 2 3 4 weights = torch.ones((2 , 10 )) * 0.1 20.0 ).reshape((2 , 10 ))1 ), values.unsqueeze(-1 ))
1 2 tensor([[[ 4.5000]],
定义模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class NWKernelRegression (nn.Module):def __init__ (self, **kwargs ):super ().__init__(**kwargs)self .w = nn.Parameter(torch.rand((1 ,), requires_grad=True ))def forward (self, queries, keys, values ):1 ]).reshape((-1 , keys.shape[1 ]))self .attention_weights = nn.functional.softmax(self .w)**2 / 2 , dim=1 )return torch.bmm(self .attention_weights.unsqueeze(1 ),1 )).reshape(-1 )
训练
将训练数据集变成“键和值”。每个训练样本都会和除本身外的键值对进行计算
1 2 3 4 5 6 7 8 1 ))1 ))1 - torch.eye(n_train)).type (torch.bool )].reshape((n_train, -1 ))1 - torch.eye(n_train)).type (torch.bool )].reshape((n_train, -1 ))
模型使用平方损失函数 + 随机梯度下降
1 2 3 4 5 6 7 8 9 10 11 12 net = NWKernelRegression() 'none' ) 0.5 ) 'epoch' , ylabel='loss' , xlim=[1 , 5 ])for epoch in range (5 ):sum ().backward()print (f'epoch {epoch + 1 } , loss {float (l.sum ()):.6 f} ' )1 , float (l.sum ()))
绘制预测结果
1 2 3 4 5 6 1 ))1 ))1 ).detach()
预测结果的曲线不是很平滑,以下绘制参数分布
1 2 3 d2l.show_heatmaps(net.attention_weights.unsqueeze(0 ).unsqueeze(0 ),'Sorted training inputs' ,'Sorted testing inputs' )
注意力评分函数
注意力评分函数 Attention Scoring Function,用来计算查询与键之间的相关性,该相关性将赋予值不同的权重,从而得到不同的上下文向量。
注意力评分函数的作用流程:
对每个查询
q i
和所有键
{ k j }
计算评分;
将评分通过 softmax 归一化为注意力权重:
α i j = exp ( score ( q i , k j ) ) ∑ j ′ exp ( score ( q i , k j ′ ) )
使用权重对值
{ v j }
加权求和,得到输出:
o i = ∑ j α i j v j
有多种注意力评分函数:
加性注意力,也即 Bahdanau 注意力;
点积注意力,Transformer 的标准选择
双线性、MLP 等;
类型
计算复杂度
是否可学习
适用场景
加性注意力
较高
是
查询/键维度不同,早期 NMT
点积注意力
低(可并行)
否(但可通过线性变换间接学习)
Transformer、高效模型
双线性/MLP
中~高
是
需要更强表达能力的任务
掩蔽 softmax 操作
屏蔽填充词元,避免它们干扰注意力的计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def masked_softmax (X, valid_lens ):"""通过在最后一个轴上掩蔽元素来执行softmax操作""" if valid_lens is None :return nn.functional.softmax(X, dim=-1 )else :if valid_lens.dim() == 1 :1 ])else :1 )1 , shape[-1 ]), valid_lens,1e6 )return nn.functional.softmax(X.reshape(shape), dim=-1 )
1 masked_softmax(torch.rand(2 , 2 , 4 ), torch.tensor([2 , 3 ]))
1 2 3 4 5 6
1 masked_softmax(torch.rand(2 , 2 , 4 ), torch.tensor([[1 , 3 ], [2 , 4 ]]))
1 2 3 4 5 tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
加性注意力
score ( q , k ) = v ⊤ tanh ( W q q + W k k )
其中:
-
q
是查询向量(Query),
k
是键向量(Key),
W q , W k
是可学习的权重矩阵,
v
是可学习的参数向量。
特点:适用于查询和键维度不同的情况,计算开销较大。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class AdditiveAttention (nn.Module):"""加性注意力""" def __init__ (self, key_size, query_size, num_hiddens, dropout, **kwargs ):super (AdditiveAttention, self ).__init__(**kwargs)self .W_k = nn.Linear(key_size, num_hiddens, bias=False )self .W_q = nn.Linear(query_size, num_hiddens, bias=False )self .w_v = nn.Linear(num_hiddens, 1 , bias=False )self .dropout = nn.Dropout(dropout)def forward (self, queries, keys, values, valid_lens ):self .W_q(queries), self .W_k(keys)2 ) + keys.unsqueeze(1 )self .w_v(features).squeeze(-1 )self .attention_weights = masked_softmax(scores, valid_lens)return torch.bmm(self .dropout(self .attention_weights), values)
k,q,v 的形状为:批量大小、步数或词元序列的长度、特征大小;
1 2 3 4 5 6 7 8 9 10 queries, keys = torch.normal(0 , 1 , (2 , 1 , 20 )), torch.ones((2 , 10 , 2 ))40 , dtype=torch.float32).reshape(1 , 10 , 4 ).repeat(2 , 1 , 1 )2 , 6 ])2 , query_size=20 , num_hiddens=8 ,0.1 )eval ()
1 2 tensor([[[ 2.0000, 3.0000, 4.0000, 5.0000]],
加性注意力支持可学习的参数,不过上面的示例每个键的值是一样的,因此注意力权重是均匀的。
1 2 d2l.show_heatmaps(attention.attention_weights.reshape((1 , 1 , 2 , 10 )),'Keys' , ylabel='Queries' )
缩放点积注意力
点积注意力的计算公式:
score ( q , k ) = q ⊤ k
缩放点积注意力公式:
score ( q , k ) = q ⊤ k d k
其中 d_k$是键向量的维度(也是查询向量的维度);使用点积的前提是 q 和 k 的维度需要相同;
之所以要使用缩放点积,是因为当
d k
比较大时,常规点积的计算结果的方差会很大,因此除以方差进行缩放,避免出现梯度消失问题。
相比加性注意力,缩放点积注意力的计算更简单高效。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class DotProductAttention (nn.Module):"""缩放点积注意力""" def __init__ (self, dropout, **kwargs ):super (DotProductAttention, self ).__init__(**kwargs)self .dropout = nn.Dropout(dropout)def forward (self, queries, keys, values, valid_lens=None ):1 ]1 ,2 )) / math.sqrt(d)self .attention_weights = masked_softmax(scores, valid_lens)return torch.bmm(self .dropout(self .attention_weights), values)
1 2 3 4 queries = torch.normal(0 , 1 , (2 , 1 , 2 ))0.5 )eval ()
1 2 tensor([[[ 2.0000, 3.0000, 4.0000, 5.0000]],
1 2 d2l.show_heatmaps(attention.attention_weights.reshape((1 , 1 , 2 , 10 )),'Keys' , ylabel='Queries' )
Bahdanau 注意力
在传统的 seq2seq 模型中,整个输入序列会转换成一个固定长度的上下文变量。解码器仅依赖这个变量计算输出。这会产生一个问题,当序列较长时,这个上下文变量不足以承担所有信息,会出现信息遗失,导致结果不准确。
Bahdanau 注意力的解决方案:解码器在计算每个输出时,额外从输入序列中提取最相关的部分,而不是只依赖一个固定的上下文向量。
计算步骤
假设:
- 编码器隐藏状态:( \mathbf{h}_1, \mathbf{h}_2, …, \mathbf{h}_T )(来自双向 RNN)
- 解码器在时间步 ( t ) 的前一隐藏状态:( \mathbf{s}_{t-1} )
步骤1:计算注意力得分
使用加性注意力函数计算注意力得分:
e t , i = v a ⊤ tanh ( W a s t − 1 + U a h i )
- ( \mathbf{W}_a, \mathbf{U}_a ):可学习的权重矩阵,用于将解码器和编码器状态映射到同一维度;
- ( \mathbf{v}_a ):可学习的权重向量,将 tanh 输出压缩为标量;
- ( e_{t,i} ):表示解码器在生成第 ( t ) 个词时,对输入第 ( i ) 个词的关注程度。
步骤2:归一化注意力权重
α t , i = exp ( e t , i ) ∑ j = 1 T exp ( e t , j )
softmax 计算
步骤3:生成上下文变量
与编码器的隐藏状态进行加权求和
c t = ∑ i = 1 T α _ t , i h _ i
c t
相当于当前步的动态摘要,从输入中读取的最相关的信息;
步骤4:解码器计算输出
将上一步的上下文变量和解码器拼接,与已输出内容
y t − 1
一起输入到预测层计算输出:
s t = RNN ( y t − 1 , [ s t − 1 ; c t ] )
y t ^ = softmax ( W y [ s t ; c t ] + b y )
优点:
缓解了输入信息的瓶颈,不再依赖固定长度的隐藏状态;
可解释性强
适用于长序列场景;
缺点:
计算开销大,因为每一步都需要与输入序列进行计算,复杂度为
O ( T ⋅ T ′ )
参数多,训练成本高,训练速度慢;
模型
1 2 3 4 5 6 7 8 9 10 11 12 import torchfrom torch import nnfrom d2l import torch as d2lclass AttentionDecoder (d2l.Decoder):"""带有注意力机制解码器的基本接口""" def __init__ (self, **kwargs ):super (AttentionDecoder, self ).__init__(**kwargs) @property def attention_weights (self ):raise NotImplementedError
上一时间步的编码器全层隐状态,将作为初始化解码器的隐状态,视为注意力的查询;
编码器在所有时间步的最终层隐状态,将作为注意力的键和值;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Seq2SeqAttentionDecoder (AttentionDecoder ):def __init__ (self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0 , **kwargs ):super (Seq2SeqAttentionDecoder, self ).__init__(**kwargs)self .attention = d2l.AdditiveAttention(self .embedding = nn.Embedding(vocab_size, embed_size)self .rnn = nn.GRU(self .dense = nn.Linear(num_hiddens, vocab_size)def init_state (self, enc_outputs, enc_valid_lens, *args ):return (outputs.permute(1 , 0 , 2 ), hidden_state, enc_valid_lens)def forward (self, X, state ):self .embedding(X).permute(1 , 0 , 2 )self ._attention_weights = [], []for x in X:1 ], dim=1 )self .attention(1 )), dim=-1 )self .rnn(x.permute(1 , 0 , 2 ), hidden_state)self ._attention_weights.append(self .attention.attention_weights)self .dense(torch.cat(outputs, dim=0 ))return outputs.permute(1 , 0 , 2 ), [enc_outputs, hidden_state, @property def attention_weights (self ):return self ._attention_weights
1 2 3 4 5 6 7 8 9 10 encoder = d2l.Seq2SeqEncoder(vocab_size=10 , embed_size=8 , num_hiddens=16 ,2 )eval ()10 , embed_size=8 , num_hiddens=16 ,2 )eval ()4 , 7 ), dtype=torch.long) None )len (state), state[0 ].shape, len (state[1 ]), state[1 ][0 ].shape
1 (torch.Size([4, 7, 10]), 3, torch.Size([4, 7, 16]), 2, torch.Size([4, 16]))
训练
1 2 3 4 5 6 7 8 9 10 11 embed_size, num_hiddens, num_layers, dropout = 32 , 32 , 2 , 0.1 64 , 10 0.005 , 250 , d2l.try_gpu()len (src_vocab), embed_size, num_hiddens, num_layers, dropout)len (tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
1 loss 0.020, 5482.1 tokens/sec on cuda:0
1 2 3 4 5 6 7 engs = ['go .' , "i lost ." , 'he\'s calm .' , 'i\'m home .' ]'va !' , 'j\'ai perdu .' , 'il est calme .' , 'je suis chez moi .' ]for eng, fra in zip (engs, fras):True )print (f'{eng} => {translation} , ' ,f'bleu {d2l.bleu(translation, fra, k=2 ):.3 f} ' )
1 2 3 4 go . => va !, bleu 1.000'ai perdu ., bleu 1.000 he' s calm . => il est riche ., bleu 0.658'm home . => je suis chez moi ., bleu 1.000
1 2 3 4 5 6 7 attention_weights = torch.cat([step[0 ][0 ][0 ] for step in dec_attention_weight_seq], 0 ).reshape((1 , 1 , -1 , num_steps))len (engs[-1 ].split()) + 1 ].cpu(),'Key positions' , ylabel='Query positions' )
多头注意力
每个注意力头相当于将数据映射到某个子空间,不同子空间关注数据的不同特征,有点像擅长不同知识领域的专家。
模型
每个注意力头的计算公式:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v
将多个注意力头进行拼接:
W o [ h 1 ⋮ h h ] ∈ R p o
实现
1 2 3 4 import mathimport torchfrom torch import nnfrom d2l import torch as d2l
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class MultiHeadAttention (nn.Module):"""多头注意力""" def __init__ (self, key_size, query_size, value_size, num_hiddens, num_heads, dropout, bias=False , **kwargs ):super (MultiHeadAttention, self ).__init__(**kwargs)self .num_heads = num_headsself .attention = d2l.DotProductAttention(dropout)self .W_q = nn.Linear(query_size, num_hiddens, bias=bias)self .W_k = nn.Linear(key_size, num_hiddens, bias=bias)self .W_v = nn.Linear(value_size, num_hiddens, bias=bias)self .W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)def forward (self, queries, keys, values, valid_lens ):self .W_q(queries), self .num_heads)self .W_k(keys), self .num_heads)self .W_v(values), self .num_heads)if valid_lens is not None :self .num_heads, dim=0 )self .attention(queries, keys, values, valid_lens)self .num_heads)return self .W_o(output_concat)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def transpose_qkv (X, num_heads ):"""为了多注意力头的并行计算而变换形状""" 0 ], X.shape[1 ], num_heads, -1 )0 , 2 , 1 , 3 )return X.reshape(-1 , X.shape[2 ], X.shape[3 ])def transpose_output (X, num_heads ):"""逆转transpose_qkv函数的操作""" 1 , num_heads, X.shape[1 ], X.shape[2 ])0 , 2 , 1 , 3 )return X.reshape(X.shape[0 ], X.shape[1 ], -1 )
1 2 3 4 num_hiddens, num_heads = 100 , 5 0.5 )eval ()
1 2 3 4 5 6 7 8 9 MultiHeadAttention(
1 2 3 4 5 batch_size, num_queries = 2 , 4 6 , torch.tensor([3 , 2 ])
自注意力和位置编码
自注意力
因为查询、键、值来自于相同的输入序列,因此称为自注意力。
1 2 3 4 import mathimport torchfrom torch import nnfrom d2l import torch as d2l
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d
1 2 3 4 num_hiddens, num_heads = 100 , 5 0.5 )eval ()
1 2 3 4 5 6 7 8 9 MultiHeadAttention(
1 2 3 batch_size, num_queries, valid_lens = 2 , 4 , torch.tensor([3 , 2 ])
比较卷积神经网络、循环神经网络和自注意力
假设卷积核为 k,输入序列长度为 n,输入和输出的通道数为 d
卷积神经网络
循环神经网络
自注意力
计算复杂度
O ( k n d 2 )
O ( n d 2 )
O ( n 2 d )
最大路径长度
O ( n / k )
O ( n )
O ( 1 )
最大路径长度取决于能否并行计算,自注意力因为没有依赖关系,能够全部并行,故为
O ( 1 )
;循环神经网络由于每一步的依赖都依赖于上一步的结果,所以无法并行计算;
位置编码
由于词元的映射存在排列不变性,即不管词元出现在序列中的哪个位置,其映射结果是一样的。显然,这种机制不符合语言规模。同一个单词,出现在句子中的不同位置,意思通常会不一样。因此需要给自注意力添加位置编码,以表示词元在序列中所处的位置。
位置编码有两种方法:
绝对位置编码
可使用正弦/余弦函数编码,偶数位用正弦,奇数位用余弦:
P E ( p o s , 2 i ) = sin ( p o s 10000 2 i / d model )
P E ( p o s , 2 i + 1 ) = cos ( p o s 10000 2 i / d model )
其中:pos 表示词元在序列中的位置,i 表示维度,取值 0 ~
d m o d e l
- 1
假设 d 取值 4,则每个 pos 的位置编码如下:
[ sin ( p o s 10000 0 ) cos ( p o s 10000 0 ) sin ( p o s 10000 1 / 2 ) cos ( p o s 10000 1 / 2 ) ] = [ sin ( p o s ) cos ( p o s ) sin ( p o s 100 ) cos ( p o s 100 ) ]
以上编码形式可以让每个位置 pos 都获得一个独特的“指纹”位置向量;
假设使用二进制来表示位置关系:
1 2 for i in range (8 ):print (f'{i} 的二进制是:{i:>03b} ' )
1 2 3 4 5 6 7 8 9
我们可以看到最低位是 0 和 1 的快速交替;第二个低位交替频率变低了;第三个低位则频率进一步降低。因此,我们可以理解,随着位置关系变长,相当于距离值增加,那么它的交替频率会变慢。正弦和余弦函数也有类似的性质,它的优点是比二进制更加节省空间,因此它的输出是浮点数;
1 2 3 P = P[0 , :, :].unsqueeze(0 ).unsqueeze(0 )'Column (encoding dimension)' ,'Row (position)' , figsize=(3.5 , 4 ), cmap='Blues' )
相对位置编码
正弦/余弦函数也可以用来计算相对位置关系。任意两个位置的相对距离,可以使用编码进行线性变换得出。因为:
sin ( a + b ) = sin a cos b + cos a sin b cos ( a + b ) = cos a cos b − sin a sin b
所以:位置 pos + k 可以表示为 pos 编码的线性函数,该线性函数的系数依赖于 k。
说人话就是,模型可以从两个位置的绝对编码中,推算出它们的相对距离。
Transformer 最初用于文本数据的序列到序列学习,但后续也广泛应用于语音、视觉等领域。
模型
Transformer 的编码器由多个相同的层堆叠组成。每个层有两个子层,分别是多头注意力 + 基于位置的前馈网络。每个子层都采用了残差连接。
基于位置的前馈网络
1 2 3 4 5 import mathimport pandas as pdimport torchfrom torch import nnfrom d2l import torch as d2l
一个两层的感知机
1 2 3 4 5 6 7 8 9 10 11 class PositionWiseFFN (nn.Module):"""基于位置的前馈网络""" def __init__ (self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs, **kwargs ):super (PositionWiseFFN, self ).__init__(**kwargs)self .dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)self .relu = nn.ReLU()self .dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)def forward (self, X ):return self .dense2(self .relu(self .dense1(X)))
1 2 3 ffn = PositionWiseFFN(4 , 4 , 8 )eval ()2 , 3 , 4 )))[0 ]
1 2 3 4 5
残差连接和层规范化
1 2 3 4 5 6 2 ) 2 ) 1 , 2 ], [2 , 3 ]], dtype=torch.float32)print ('layer norm:' , ln(X), '\nbatch norm:' , bn(X))
1 2 3 4 layer norm: tensor([[-1.0000, 1.0000],
1 2 3 4 5 6 7 8 9 10 class AddNorm (nn.Module):"""残差连接后进行层规范化""" def __init__ (self, normalized_shape, dropout, **kwargs ):super (AddNorm, self ).__init__(**kwargs)self .dropout = nn.Dropout(dropout)self .ln = nn.LayerNorm(normalized_shape)def forward (self, X, Y ):return self .ln(self .dropout(Y) + X)
1 2 3 add_norm = AddNorm([3 , 4 ], 0.5 )eval ()2 , 3 , 4 )), torch.ones((2 , 3 , 4 ))).shape
编码器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class EncoderBlock (nn.Module):"""Transformer编码器块""" def __init__ (self, key_size, query_size, value_size, num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, dropout, use_bias=False , **kwargs ):super (EncoderBlock, self ).__init__(**kwargs)self .attention = d2l.MultiHeadAttention(self .addnorm1 = AddNorm(norm_shape, dropout)self .ffn = PositionWiseFFN(self .addnorm2 = AddNorm(norm_shape, dropout)def forward (self, X, valid_lens ):self .addnorm1(X, self .attention(X, X, X, valid_lens))return self .addnorm2(Y, self .ffn(Y))
1 2 3 4 5 X = torch.ones((2 , 100 , 24 ))3 , 2 ])24 , 24 , 24 , 24 , [100 , 24 ], 24 , 48 , 8 , 0.5 )eval ()
1 torch.Size([2, 100, 24])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class TransformerEncoder (d2l.Encoder):"""Transformer编码器""" def __init__ (self, vocab_size, key_size, query_size, value_size, num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, num_layers, dropout, use_bias=False , **kwargs ):super (TransformerEncoder, self ).__init__(**kwargs)self .num_hiddens = num_hiddensself .embedding = nn.Embedding(vocab_size, num_hiddens)self .pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)self .blks = nn.Sequential()for i in range (num_layers):self .blks.add_module("block" +str (i),def forward (self, X, valid_lens, *args ):self .pos_encoding(self .embedding(X) * math.sqrt(self .num_hiddens))self .attention_weights = [None ] * len (self .blks)for i, blk in enumerate (self .blks):self .attention_weights[return X
1 2 3 4 encoder = TransformerEncoder(200 , 24 , 24 , 24 , 24 , [100 , 24 ], 24 , 48 , 8 , 2 , 0.5 )eval ()2 , 100 ), dtype=torch.long), valid_lens).shape
1 torch.Size([2, 100, 24])
解码器
之所以需要掩蔽,是因为每个时间步是在上一个时间步的基础上计算的,因此在预测阶段,需要先掩蔽后续时间步的值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class DecoderBlock (nn.Module):"""解码器中第i个块""" def __init__ (self, key_size, query_size, value_size, num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, dropout, i, **kwargs ):super (DecoderBlock, self ).__init__(**kwargs)self .i = iself .attention1 = d2l.MultiHeadAttention(self .addnorm1 = AddNorm(norm_shape, dropout)self .attention2 = d2l.MultiHeadAttention(self .addnorm2 = AddNorm(norm_shape, dropout)self .ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,self .addnorm3 = AddNorm(norm_shape, dropout)def forward (self, X, state ):0 ], state[1 ]if state[2 ][self .i] is None :else :2 ][self .i], X), axis=1 )2 ][self .i] = key_valuesif self .training:1 , num_steps + 1 , device=X.device).repeat(batch_size, 1 )else :None self .attention1(X, key_values, key_values, dec_valid_lens)self .addnorm1(X, X2)self .attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)self .addnorm2(Y, Y2)return self .addnorm3(Z, self .ffn(Z)), state
1 2 3 4 5 decoder_blk = DecoderBlock(24 , 24 , 24 , 24 , [100 , 24 ], 24 , 48 , 8 , 0.5 , 0 )eval ()2 , 100 , 24 ))None ]]0 ].shape
1 torch.Size([2, 100, 24])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class TransformerDecoder (d2l.AttentionDecoder):def __init__ (self, vocab_size, key_size, query_size, value_size, num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, num_layers, dropout, **kwargs ):super (TransformerDecoder, self ).__init__(**kwargs)self .num_hiddens = num_hiddensself .num_layers = num_layersself .embedding = nn.Embedding(vocab_size, num_hiddens)self .pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)self .blks = nn.Sequential()for i in range (num_layers):self .blks.add_module("block" +str (i),self .dense = nn.Linear(num_hiddens, vocab_size)def init_state (self, enc_outputs, enc_valid_lens, *args ):return [enc_outputs, enc_valid_lens, [None ] * self .num_layers]def forward (self, X, state ):self .pos_encoding(self .embedding(X) * math.sqrt(self .num_hiddens))self ._attention_weights = [[None ] * len (self .blks) for _ in range (2 )]for i, blk in enumerate (self .blks):self ._attention_weights[0 ][self ._attention_weights[1 ][return self .dense(X), state @property def attention_weights (self ):return self ._attention_weights
训练
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 num_hiddens, num_layers, dropout, batch_size, num_steps = 32 , 2 , 0.1 , 64 , 10 0.005 , 200 , d2l.try_gpu()32 , 64 , 4 32 , 32 , 32 32 ]len (src_vocab), key_size, query_size, value_size, num_hiddens,len (tgt_vocab), key_size, query_size, value_size, num_hiddens,
1 loss 0.032, 5679.3 tokens/sec on cuda:0
1 2 3 4 5 6 7 8 'go .' , "i lost ." , 'he\'s calm .' , 'i\'m home .' ]'va !' , 'j\'ai perdu .' , 'il est calme .' , 'je suis chez moi .' ]for eng, fra in zip (engs, fras):True )print (f'{eng} => {translation} , ' ,f'bleu {d2l.bleu(translation, fra, k=2 ):.3 f} ' )
1 2 3 4 go . => va !, bleu 1.000'ai perdu ., bleu 1.000 he' s calm . => il est calme ., bleu 1.000'm home . => je suis chez moi ., bleu 1.000
1 2 3 enc_attention_weights = torch.cat(net.encoder.attention_weights, 0 ).reshape((num_layers, num_heads,1 , num_steps))
1 torch.Size([2, 4, 10, 10])
1 2 3 4 d2l.show_heatmaps('Key positions' ,'Query positions' , titles=['Head %d' % i for i in range (1 , 5 )],7 , 3.5 ))
1 2 3 4 5 6 7 8 9 dec_attention_weights_2d = [head[0 ].tolist()for step in dec_attention_weight_seqfor attn in step for blk in attn for head in blk]0.0 ).values)1 , 2 , num_layers, num_heads, num_steps))1 , 2 , 3 , 0 , 4 )
1 (torch.Size([2, 4, 6, 10]), torch.Size([2, 4, 6, 10]))
1 2 3 4 d2l.show_heatmaps(len (translation.split()) + 1 ],'Key positions' , ylabel='Query positions' ,'Head %d' % i for i in range (1 , 5 )], figsize=(7 , 3.5 ))
1 2 3 4 d2l.show_heatmaps('Key positions' ,'Query positions' , titles=['Head %d' % i for i in range (1 , 5 )],7 , 3.5 ))
优化算法
优化和深度学习
先定损失函数,再定优化算法。因此损失函数也称为优化问题的目标函数。
优化的目标
优化算法的目标是最小化损失函数的值;深度学习的目标是在有限的数据集下,找到预测能力最好的模型。二者的目标不完全相同。满足前者不代表满足后者,例如出现过拟合。
两个概念:
经验风险:训练数据集的平均损失;
风险:所有数据的预期损失;
这两个风险不一定相同,示例如下:
优化的挑战
深度学习中的绝大多数目标函数都比较复杂,不存在解析解,因此需要使用数值优化算法。以下是一些常见的挑战。
局部最小值
一定程度的噪声有助于让参数逃离局部最小值,这也是小批量随机梯度下降算法能够有效的原因之一。
鞍点
梯度消失的点,既不是最小值,也不是最大值;以下是三维空间的鞍点示例:
梯度消失
局部最小值也不一定是不可接受,在某些应用场景下有可能也是够用的。当遇到梯度消失时,优化有可能会卡住,迟迟不能取得进展,此时重新初始化参数有可能会有帮助。另外,好的初始化参数也很重要,可以少走弯路。
凸性
定义
凸集
对于任意属于 X 集合的两个点 a 和 b,如果 a 和 b 连线上的点,也属于 X 集合。那么可以称 X 集合是一个凸集。
如果 X 和 Y 是凸集,那么 X 和 Y 的交集也是凸集。
但是两个凸集的并集则不一定是凸集。
凸函数
以下三种函数的凸性,分别是:凸、非凸、凸;
詹森不等式:它是数学分析和概率论中的一个概念,用来描述凸函数和期望之间的关系。函数在期望处的值,不大于期望在函数处的值。
离散形式(加权平均)
f ( ∑ i = 1 n λ i x i ) ≤ ∑ i = 1 n λ i f ( x i )
其中:
∑ i = 1 n λ i = 1
概率形式(期望形式)
如果 f 是凸函数:
f ( E [ X ] ) ≤ E [ f ( X ) ]
如果 f 是凹函数:
f ( E [ X ] ) ≥ E [ f ( X ) ]
性质
局部最小值是全局最小值
凸函数的下水平集是凸的
若 f 是凸函数,则对于任意的
α ∈ R
,其下水平集
S α
是凸集。
凸性和二阶层数
当一个函数存在二阶层数时,我们可以很容易的检查这个函数是否为凸的。
约束
拉格朗日函数
拉格朗日函数的鞍点是原始优化问题的最优解。
梯度下降
一维梯度下降
通过多轮迭代,梯度下降能够慢慢接近最优解
太小的学习率会导致收敛很慢
太大的学习率则可能导致发散,无法收敛
高学习率有可能导致局部最小值;
多元梯度下降
多元梯度下降原理和一维梯度下降类似,只是梯度变成了由多个变量的偏导数组成:
∇ f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , … , ∂ f ( x ) ∂ x d ] ⊤
自适应方法
根据 delta 给出的方向,进行二分搜索,找到最合适的学习率
随机梯度下降
随机梯度更新
当使用标准梯度下降时,损失是取全部样本的平均值:
f ( x ) = 1 n ∑ i = 1 n f i ( x )
∇ f ( x ) = 1 n ∑ i = 1 n ∇ f i ( x )
因此当训练数据集的样本数量 n 比较大时,计算的代价也随之线性增长。随机梯度下降的原理是不计算平均值,而根据当前单个样本的梯度下降进行更新
x ← x − η ∇ f i ( x )
这样计算代价由 O(n) 变成了 O(1) 了;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import mathimport torchfrom d2l import torch as d2ldef f (x1, x2 ): return x1 ** 2 + 2 * x2 ** 2 def f_grad (x1, x2 ): return 2 * x1, 4 * x2def sgd (x1, x2, s1, s2, f_grad ):0.0 , 1 , (1 ,))0.0 , 1 , (1 ,))return (x1 - eta_t * g1, x2 - eta_t * g2, 0 , 0 )def constant_lr ():return 1 0.1 50 , f_grad=f_grad))
1 epoch 50, x1: 0.020569, x2: 0.227895
动态学习率
有几种动态调整学习率的策略,包括:
分段常数:
η ( t ) = η i if t i ≤ t ≤ t i + 1
指数衰减:
η ( t ) = η 0 ⋅ e − λ t
多项式衰减:
η ( t ) = η 0 ⋅ ( β t + 1 ) − α
1 2 3 4 5 6 7 8 9 10 def exponential_lr ():global t1 return math.exp(-0.1 * t)1 1000 , f_grad=f_grad))
1 2 3 4 5 6 7 8 9 10 def polynomial_lr ():global t1 return (1 + 0.1 * t) ** (-0.5 )1 50 , f_grad=f_grad))
小批量随机梯度下降
小批量有助于提高计算效率,一方面是因为可以利用向量化和缓存,另一方面是无须全局求梯度,只需要局部求梯度即可更新参数,计算的工作量大大减少。虽然它会带来一点点的误差,但可以忽略不计,同时可以得到更快的收敛速度和更高的计算效率。
动量法
小批量梯度下降有时候会遇到局部最小值的问题(例如遇到峡谷),动量法通过引入额外的“速度”参数,用来累积过去的梯度,相当于使用过往梯度的滑动平均值,它有以下好处:
当梯度方向一 致时,速度会累积,收敛会加快;
当梯度方向不一致时,速度会抵消,从而减少震荡;
AdaGrad 算法
模型在学习特征时,有些特征是常见的,有些特征是罕见的(稀疏特征)。如果它们共用一个学习率的话,容易导致学习的进度不均匀。一些常见的特征很快就学会了,一些罕见的特征即使训练了很久,也没有找到最佳参数值。
AdaGrad 算法的核心思想是给不同的特征分配不同的学习率:
更新频繁的参数,说明很敏感,降低学习率;
更新不频繁的参数,说明不敏感,提高学习率;
通过区别对待,有助于加快稀疏特征的收敛,同时避免给常见特征带来扰动。
优点:
缺点:
学习率单调递减,由于历史梯度不断累积,分母越来越大,学习率越来越小,有可能导致训练过早停止;
后期梯度消失,参数不再更新,过早出现收敛;
计算公式:
s t = s t − 1 + g t 2
RMSProp 算法
RMSProp 算法是对 AdaGrad 算法的改进,以避免过早出现梯度消失的问题。RMSProp 使用历史梯度平方的滑动平均值,这样就可以避免 AdaGrad 遇到的分母膨胀问题了。
与 AdaGrad 的区别:
AdaGrad 累加了所在历史梯度的平方,因此分母很大变大,容易过早出现梯度消失;
RMSProp 使用指数衰减平均,更注重近期梯度;
s t ← γ s t − 1 + ( 1 − γ ) g t 2
其中 ( \rho ) 是衰减率(通常取 0.9)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import mathimport torchfrom d2l import torch as d2ldef rmsprop_2d (x1, x2, s1, s2 ):0.2 * x1, 4 * x2, 1e-6 1 - gamma) * g1 ** 2 1 - gamma) * g2 ** 2 return x1, x2, s1, s2def f_2d (x1, x2 ):return 0.1 * x1 ** 2 + 2 * x2 ** 2 0.4 , 0.9
Adadelta 算法
Adadelta 算法也是对 AdaGrad 算法的一种改进,它的核心思想和 RMSProp 类似,使用指数滑动平均值,同时还引入参数更新量的滑动平方的均值;
s t = ρ s t − 1 + ( 1 − ρ ) g t 2 .
x t = x t − 1 − g t ′
$$
\mathbf{g}_t' = \frac{\sqrt{\Delta\mathbf{x}_{t-1} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t
$$
Δ x t = ρ Δ x t − 1 + ( 1 − ρ ) g t ′ 2
优点
无需设置学习率,会自动调整;
缓解了学习率过快衰减的问题;
缺点:
收敛速度不如 Adam;
需要维护两个均值,实现起来稍复杂一些;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import torchfrom d2l import torch as d2ldef init_adadelta_states (feature_dim ):1 )), torch.zeros(1 )1 )), torch.zeros(1 )return ((s_w, delta_w), (s_b, delta_b))def adadelta (params, states, hyperparams ):'rho' ], 1e-5 for p, (s, delta) in zip (params, states):with torch.no_grad():1 - rho) * torch.square(p.grad)1 - rho) * g * g
1 2 3 data_iter, feature_dim = d2l.get_data_ch11(batch_size=10 )'rho' : 0.9 }, data_iter, feature_dim);
Adam 算法
Adam 算法综合了动量法和 RMSProp 两个算法的优点。它的核心是使用指数滑动平均法来计算动量(均值)和二次矩(方差):
v t ← β 1 v t − 1 + ( 1 − β 1 ) g t , s t ← β 2 s t − 1 + ( 1 − β 2 ) g t 2 .
其中
β 1
和
β 2
是非负加权参数(衰减率),通常取值
β 1 = 0.9
和
β 2 = 0.999
,因此方差的移动速度要比均值的移动速度小得多(小了几个数量级,一个是 0.1, 一个是 0.001 ,差了 100 倍);
注:一阶中心矩是均值;二阶中心矩是方差;
修正偏差:
v ^ t = v t 1 − β 1 t , s ^ t = s t 1 − β 2 t
更新参数:
θ t = θ t − 1 − α ⋅ v ^ t s ^ t + ϵ
其中
α
是学习率;
优点:
自适应学习率,不同的参数学习率不同;
通过动量加速收敛,减少了震荡;
能够有效处理稀疏特征;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 import torchfrom d2l import torch as d2ldef init_adam_states (feature_dim ):1 )), torch.zeros(1 )1 )), torch.zeros(1 )return ((v_w, s_w), (v_b, s_b))def adam (params, states, hyperparams ):0.9 , 0.999 , 1e-6 for p, (v, s) in zip (params, states):with torch.no_grad():1 - beta1) * p.grad1 - beta2) * torch.square(p.grad)1 - beta1 ** hyperparams['t' ])1 - beta2 ** hyperparams['t' ])'lr' ] * v_bias_corr / (torch.sqrt(s_bias_corr)'t' ] += 1
1 2 3 data_iter, feature_dim = d2l.get_data_ch11(batch_size=10 )'lr' : 0.01 , 't' : 1 }, data_iter, feature_dim);
1 2 3 'lr' : 0.01 }, data_iter)
Yogi
由于 Adam 中的二阶矩(方差)是单调递增的,因此有可能会出现爆炸,届时会导致 Adam 算法无法收敛。Yogi 的核心思想是改进二阶矩的计算方式,让它既可以变大,也可以变小,而不是单向的,这样能够更准确的反映当前梯度的方差。
v t = v t − 1 + ( 1 − β 2 ) ⋅ sign ( g t 2 − v t − 1 ) ⋅ g t 2
相比原始的 Adam 算法,增加了一个
sign ( g t 2 − v t − 1 )
,它的作用是:
当
g t 2
比
v t − 1
大时,则增加
v t
当
g t 2
比
v t − 1
小时,则减少
v t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def yogi (params, states, hyperparams ):0.9 , 0.999 , 1e-3 for p, (v, s) in zip (params, states):with torch.no_grad():1 - beta1) * p.grad1 - beta2) * torch.sign(1 - beta1 ** hyperparams['t' ])1 - beta2 ** hyperparams['t' ])'lr' ] * v_bias_corr / (torch.sqrt(s_bias_corr)'t' ] += 1 10 )'lr' : 0.01 , 't' : 1 }, data_iter, feature_dim);
学习率调度器
学习率可以由各种优化器的算法进行自适应调整,也可以指定手动指定调整的策略,例如多项式衰减、分段常量+乘法衰减、余弦调度器等;
余弦调度器
η t = η T + η 0 − η T 2 ( 1 + cos ( π t / T ) )
其中:
T
表示步数,
η T
表示第 T 步时的学习率;
据说余弦调度器在一些机器视觉的场景中效果很好;
预热
如果初始学习率过小,有可能收敛很慢;如果初始学习率太大,有可能一开始就发散。一种解决方案是设置一个预热期。在预热期间,设置学习率慢慢增加到最大值,然后再慢慢冷却,示意图如下:
计算性能
编译器和解释器
Python 是一解释器语言,其代码的执行依赖于解释器的逐行解释。显然这不是一种高效的办法,因为逐行解释无法站在更宏观的视角对代码进行优化。这种优化是那些使用编译器的语言在性能上的天然优势。
符号式编程
符号式编程是解决以上问题的一种策略,它将定义好的代码进行提前编译,此时可以很方便的进行优化。之后在执行时,调用已经提前编译好的程序,从而加快计算的速度。缺点是不如命令式编程来得直观。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 def add_ ():return ''' def add(a, b): return a + b ''' def fancy_func_ ():return ''' def fancy_func(a, b, c, d): e = add(a, b) f = add(c, d) g = add(e, f) return g ''' def evoke_ ():return add_() + fancy_func_() + 'print(fancy_func(1, 2, 3, 4))' print (prog)compile (prog, '' , 'exec' )exec (y)
混合式编程
Theano、Tensorflow/Keras 走的是符号式编程路线,之后也增加了命令式编程的支持。Pytorch 则走的是命令式编程路线,之后引入 TorchScript 支持将命令式编程转成符号式程序,相当于提前进行编译,这样在运行时就不需要 Python 解释器了。
PyTorch 2.x 版本引入了 compile 编译优化功能,可以不使用 TorchScript 优化。
Sequential 的混合式编程
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import torchfrom torch import nnfrom d2l import torch as d2ldef get_net ():512 , 256 ),256 , 128 ),128 , 2 ))return net1 , 512 ))
对模型和参数进行提前编译还有一个好处,是让模型的迁移变得更简单了。序列化后的模型,其执行不再依赖于 Python环境。
异步计算
Python 本身是单线程的,因此不擅于处理并行运算,除非借助外部工具。PyTorch 的解决办法是分离前后端,后端执行真正的计算,它由 C++ 实现。前端主要负责发出任务,实现语言可以是 Python、C++、Scala、Rust 等;
后端的计算是异步的,因此前端需要等待后端最终返回计算结果。但前端可以将所有任务一次性发给后端,由后端进行编排实现并行计算。待计算完成后,前端从后端取回最终的结果即可。在中间计算的过程中,后端无须返回结果给前端。
自动并行
当有多张 GPU 显卡时,可以将张量分布在不同的显卡上。当调用相同的函数,对张量进行计算时,这些计算是可以自动并行的。框架不会等一个张量计算完毕后,再去计算另外一个,而是异步和同时开始的。最终可以通过 torch.cuda.synchronize 来同步计算结果。
PyTorch 还支持将 GPU 上的计算结果并行同步到 CPU,同步并不需要等待 GPU 完成所有计算,可以先同步已经计算完成的部分,毕竟 GPU 内部也是无数个小的计算单元。每个计算单元可以在自己的数据计算结束后,同步结果给 CPU,无须等待其他计算单元完成计算再同步。
以下是一个分布计算的多层感知机,两个 GPU 各负责计算一部分数据,并将结果同步到 CPU,以便 CPU 完成累加。之后 CPU 将累积的结果返回给 GPU 继续下一轮的计算。
硬件
CPU 和 GPU 一般使用高速 PCIe 通道进行数据传输。 现代 CPU 都添加了向量处理单元,能够高效的并行处理一些向量运算。
GPU 主要是为大吞吐量的并行计算,因此它不太擅长处理稀疏矩阵和中断操作。在处理这两种场景时,会显著出现资源闲置。
单台设备上的多张 GPU 之间,有两种常见的数据同步机制,分别是 PCIe 和 NVLink;如果是不同设备之间,则一般使用有线网络和交换机,但典型带宽为 1GBit/s,相比前一种机制,差了 1~2 个数量级;
多 GPU 训练
问题拆分
几种拆分思路:
拆分模型:每个 GPU 负责模型中的一个或多个层;优点:可以训练大模型;缺点:不适合 GPU 间需要大量数据传输的场景;
拆分层:例如 64 通道的输出,由每个 GPU 负责其中的 16 个通道;优缺点同上,数据同步是一个问题;
拆分数据:每个 GPU 都包含整个网络,但只负责计算一部分数据;优点:很通用,同步工作量很小;缺点:无法训练大模型;
数据并行性
优点:可以很方便的扩大小批量的单批数量,该数量需要是 GPU 数量的倍数,以便能够平摊工作量;
简单网络
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 0.01 20 , 1 , 3 , 3 )) * scale20 )50 , 20 , 5 , 5 )) * scale50 )800 , 128 )) * scale128 )128 , 10 )) * scale10 )def lenet (X, params ):input =X, weight=params[0 ], bias=params[1 ])input =h1_activation, kernel_size=(2 , 2 ), stride=(2 , 2 ))input =h1, weight=params[2 ], bias=params[3 ])input =h2_activation, kernel_size=(2 , 2 ), stride=(2 , 2 ))0 ], -1 )4 ]) + params[5 ]6 ]) + params[7 ]return y_hat'none' )
数据同步
1 2 3 4 5 6 def get_params (params, device ):for p in params]for p in new_params:return new_params
1 2 3 4 5 6 new_params = get_params(params, d2l.try_gpu(0 ))print ('b1 权重:' , new_params[1 ])print ('b1 梯度:' , new_params[1 ].grad)
1 2 3 4 5 6 def allreduce (data ):for i in range (1 , len (data)):0 ][:] += data[i].to(data[0 ].device)for i in range (1 , len (data)):0 ].to(data[i].device)
1 2 3 4 data = [torch.ones((1 , 2 ), device=d2l.try_gpu(i)) * (i + 1 ) for i in range (2 )]print ('allreduce之前:\n' , data[0 ], '\n' , data[1 ])print ('allreduce之后:\n' , data[0 ], '\n' , data[1 ])
1 2 3 4 5 6 allreduce之前:'cuda:0' ) 'cuda:1' )'cuda:0' ) 'cuda:1' )
数据分发
1 2 3 4 5 6 data = torch.arange(20 ).reshape(4 , 5 )'cuda:0' ), torch.device('cuda:1' )]print ('input :' , data)print ('load into' , devices)print ('output:' , split)
1 2 3 4 5 6 7 8 input : tensor([[ 0, 1, 2, 3, 4],type ='cuda' , index=0), device(type ='cuda' , index=1)]'cuda:0' ), tensor([[10, 11, 12, 13, 14],'cuda:1' ))
1 2 3 4 5 def split_batch (X, y, devices ):"""将X和y拆分到多个设备上""" assert X.shape[0 ] == y.shape[0 ]return (nn.parallel.scatter(X, devices),
训练
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def train_batch (X, y, device_params, devices, lr ):sum ()for X_shard, y_shard, device_W in zip (for l in ls: with torch.no_grad():for i in range (len (device_params[0 ])):for c in range (len (devices))])for param in device_params:0 ])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def train (num_gpus, batch_size, lr ):for i in range (num_gpus)]for d in devices]10 'epoch' , 'test acc' , xlim=[1 , num_epochs])for epoch in range (num_epochs):for X, y in train_iter:1 , (d2l.evaluate_accuracy_gpu(lambda x: lenet(x, device_params[0 ]), test_iter, devices[0 ]),))print (f'测试精度:{animator.Y[0 ][-1 ]:.2 f} ,{timer.avg():.1 f} 秒/轮,' f'在{str (devices)} ' )
1 2 3 1 , batch_size=256 , lr=0.2 )
1 2 3 2 , batch_size=256 , lr=0.2 )
由于模型和数据量都很小,训练结果并没有体现任何速度上的提升;
多 GPU 简洁实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 import torchfrom torch import nnfrom d2l import torch as d2ldef resnet18 (num_classes, in_channels=1 ):"""稍加简化的ResNet-18模型""" def resnet_block (in_channels, out_channels, num_residuals, first_block=False ):for i in range (num_residuals):if i == 0 and not first_block:True , strides=2 ))else :return nn.Sequential(*blk)64 , kernel_size=3 , stride=1 , padding=1 ),64 ),"resnet_block1" , resnet_block(64 , 64 , 2 , first_block=True ))"resnet_block2" , resnet_block(64 , 128 , 2 ))"resnet_block3" , resnet_block(128 , 256 , 2 ))"resnet_block4" , resnet_block(256 , 512 , 2 ))"global_avg_pool" , nn.AdaptiveAvgPool2d((1 ,1 )))"fc" , nn.Sequential(nn.Flatten(),512 , num_classes)))return net
1 2 3 net = resnet18(10 )
训练
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def train (net, num_gpus, batch_size, lr ):for i in range (num_gpus)]def init_weights (m ):if type (m) in [nn.Linear, nn.Conv2d]:0.01 )10 'epoch' , 'test acc' , xlim=[1 , num_epochs])for epoch in range (num_epochs):for X, y in train_iter:0 ]), y.to(devices[0 ])1 , (d2l.evaluate_accuracy_gpu(net, test_iter),))print (f'测试精度:{animator.Y[0 ][-1 ]:.2 f} ,{timer.avg():.1 f} 秒/轮,' f'在{str (devices)} ' )
1 2 3 1 , batch_size=256 , lr=0.1 )
1 2 3 2 , batch_size=512 , lr=0.2 )
ResNet 模型比 LeNet 更复杂一些,此时多 GPU 并行开始体现一些速度上的优势;
参数服务器
数据并行训练
分布于 GPU 上的参数有多种同步策略:
统一和 CPU 同步;
与某个指定的 GPU 同步;
各 GPU 之间相互同步;
环同步
为提升参数同步速度,一些硬件会添加定制连接,例如使用 NVLink;
当拥有多张 GPU 时,需要设计合适的同步策略,以最小化同步的时间成本。常规同步机制因为某一时刻只有一个 NVLink 通道在同步,其他通道处于闲置状态,所以效率很低。更好的办法同时启用每个同步通道。每个 GPU 每次通过同步向其左边的 GPU 同步自己的当前已经拥有的数据(它会动态更新,因为每一轮都会有右边 GPU 同步的新数据进来);
以上环同步示例通过第一阶段的 3 轮(4张GPU - 1)同步,让每个 GPU 都拥有一个完整的行向量;之后再通过第二阶段的 3 轮同步,每一轮同步一次行向量,就可以让所有的 GPU 所有完整的数据;
多机训练
对于多台服务器,不得不考虑有限网络带宽带来的通信成本。为降低带宽瓶颈,一种方法是增加多个服务器节点,每个服务器只负责部分数据的读取,类似于常规网盘的多节点下载。
键值存储
每台设备的每个 GPU 只负责计算一部分数据,之后它提交计算结果,并最终获得返回的聚合结果(累加或求平均)。这种工作模式很像 GPU 内部的计算单元分工,也很像常见的集群分布式计算。因此它可以通过类似 push-pull 的机制来进行抽象。以便让模型开发人员和系统架构师之间的工作尽量解耦。
计算机视觉
图像增广
图像增广的好处:
扩大数据集规模
提高模型的泛化能力,减少对某些特征的过度依赖;
图像增广的方法:
旋转;
改变颜色:亮度、对比度、饱和度、色调等;
变形;
裁剪;
翻转
合成
微调
微调包括:
微调特征层的参数(使用较小的学习率);
重新训练输出层参数;
目标检测和边界框
边界框用于表示目标的位置,有两种表示方法:
左上角坐标 + 右下角坐标;
中心点坐标 + 宽度 + 高度;
锚框
锚框:以某个像素为中心,按不同的宽高比和缩放比,生成不同的边界框;用于采样,以便判断该区域是否包括目标物体。并且还可以不断逼近,以便获取目标所在位置的准确值。
交并比
交并比:交集 / 并集;交并比越大,说明重叠部分越多,预测越准确。
比较锚框和真实边界框重叠区域的比例;
可使用非极大值抑制去除重叠的边框
多尺度目标检测
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchfrom d2l import torch as d2l'../img/catdog.jpg' )2 ]def display_anchors (fmap_w, fmap_h, s ):1 , 10 , fmap_h, fmap_w))1 , 2 , 0.5 ])0 ] * bbox_scale)
1 display_anchors(fmap_w=4 , fmap_h=4 , s=[0.15 ])
1 2 2 , fmap_h=2 , s=[0.4 ])
1 2 1 , fmap_h=1 , s=[0.8 ])
模型需要预测每组锚框的类别和偏移量,不同组的锚框有不同的中心。
深层神经网络每个层的感受野不同,因为不同层可以用来检测不同大小的目标。
目标检测数据集
模拟香蕉的检测,将香蕉的图片,合成到一些其他图片中
单发多框检测 SSD
模型
类别预测层
假设目标的类型数量为
q
,那么加上背景,总共有
q + 1
个类型;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import torchimport torchvisionfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2l""" 类别预测函数 num_anchors 某一点的锚框数量 num_classes 类别数量,不包含背景 使用通道数来表示某一点所有锚框的类别概率分布 """ def cls_predictor (num_inputs, num_anchors, num_classes ):return nn.Conv2d(num_inputs, num_anchors * (num_classes + 1 ),3 , padding=1 )
边界框预测层
1 2 3 4 5 6 """ bbox 锚框位置预测函数 每个锚框预测 4 个偏移量,分别是 x, y, w, h 等四个值的偏移量 """ def bbox_predictor (num_inputs, num_anchors ):return nn.Conv2d(num_inputs, num_anchors * 4 , kernel_size=3 , padding=1 )
连结多尺度的预测
1 2 3 4 5 6 7 8 def forward (x, block ):return block(x) 2 , 8 , 20 , 20 )), cls_predictor(8 , 5 , 10 )) 2 , 16 , 10 , 10 )), cls_predictor(16 , 3 , 10 ))
1 2 3 4
为了将不同尺度的预测输出链接起来,需要对张量格式进行转换,转成(批量大小,通道数 x 高度 x 宽度)
1 2 3 4 5 6 7 8 def flatten_pred (pred ):return torch.flatten(pred.permute(0 , 2 , 3 , 1 ), start_dim=1 )def concat_preds (preds ):return torch.cat([flatten_pred(p) for p in preds], dim=1 )
1 concat_preds([Y1, Y2]).shape
高和宽减半块
1 2 3 4 5 6 7 8 9 10 11 def down_sample_blk (in_channels, out_channels ):for _ in range (2 ): 两个块,每个块包含卷积 + 批量规范化 + 激活三个层3 , padding=1 ))2 )) return nn.Sequential(*blk)
1 forward(torch.zeros((2 , 3 , 20 , 20 )), down_sample_blk(3 , 10 )).shape
1 torch.Size([2, 10, 10, 10])
基本网络块
1 2 3 4 5 6 7 8 9 def base_net ():3 , 16 , 32 , 64 ] for i in range (len (num_filters) - 1 ):1 ]))return nn.Sequential(*blk)2 , 3 , 256 , 256 )), base_net()).shape
1 2 torch.Size([2, 64, 32, 32])
完整的模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def get_blk (i ):if i == 0 :elif i == 1 :64 , 128 )elif i == 4 :1 ,1 ))else :128 , 128 )return blk
为模块定义前向传播方法,因为需要在不同尺度的上面进行预测,以便获得不同大小的目标的类型和位置;
1 2 3 4 5 6 def blk_forward (X, blk, size, ratio, cls_predictor, bbox_predictor ):return (Y, anchors, cls_preds, bbox_preds)
1 2 3 4 5 6 0.2 , 0.272 ], [0.37 , 0.447 ], [0.54 , 0.619 ], [0.71 , 0.79 ],0.88 , 0.961 ]]1 , 2 , 0.5 ]] * 5 len (sizes[0 ]) + len (ratios[0 ]) - 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class TinySSD (nn.Module):def __init__ (self, num_classes, **kwargs ):super (TinySSD, self ).__init__(**kwargs)self .num_classes = num_classes64 , 128 , 128 , 128 , 128 ]for i in range (5 ):setattr (self , f'blk_{i} ' , get_blk(i))setattr (self , f'cls_{i} ' , cls_predictor(idx_to_in_channels[i],setattr (self , f'bbox_{i} ' , bbox_predictor(idx_to_in_channels[i],def forward (self, X ):None ] * 5 , [None ] * 5 , [None ] * 5 for i in range (5 ):getattr (self , f'blk_{i} ' ), sizes[i], ratios[i],getattr (self , f'cls_{i} ' ), getattr (self , f'bbox_{i} ' ))print (X.shape) 1 )0 ], -1 , self .num_classes + 1 )return anchors, cls_preds, bbox_preds
1 2 3 4 5 6 7 net = TinySSD(num_classes=1 )32 , 3 , 256 , 256 )) print ('output anchors:' , anchors.shape)print ('output class preds:' , cls_preds.shape)print ('output bbox preds:' , bbox_preds.shape)
1 2 3 4 5 6 7 8 9 10
训练模型
读取数据集和初始化
1 2 batch_size = 32
1 2 read 1000 training examplesread 100 validation examples
1 2 device, net = d2l.try_gpu(), TinySSD(num_classes=1 )0.2 , weight_decay=5e-4 )
定义损失函数和评估函数
1 2 3 4 5 6 7 8 9 10 cls_loss = nn.CrossEntropyLoss(reduction='none' )'none' )def calc_loss (cls_preds, cls_labels, bbox_preds, bbox_labels, bbox_masks ):0 ], cls_preds.shape[2 ]1 , num_classes),1 )).reshape(batch_size, -1 ).mean(dim=1 )1 )return cls + bbox
1 2 3 4 5 6 7 8 def cls_eval (cls_preds, cls_labels ):return float ((cls_preds.argmax(dim=-1 ).type (sum ())def bbox_eval (bbox_preds, bbox_labels, bbox_masks ):return float ((torch.abs ((bbox_labels - bbox_preds) * bbox_masks)).sum ())
训练模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 num_epochs, timer = 20 , d2l.Timer()'epoch' , xlim=[1 , num_epochs],'class error' , 'bbox mae' ])for epoch in range (num_epochs):4 )for features, target in train_iter:1 - metric[0 ] / metric[1 ], metric[2 ] / metric[3 ]1 , (cls_err, bbox_mae))print (f'class err {cls_err:.2 e} , bbox mae {bbox_mae:.2 e} ' )print (f'{len (train_iter.dataset) / timer.stop():.1 f} examples/sec on ' f'{str (device)} ' )
1 2 class err 3.17e-03, bbox mae 3.01e-03
预测目标
1 2 X = torchvision.io.read_image('../img/banana.jpg' ).unsqueeze(0 ).float ()0 ).permute(1 , 2 , 0 ).long()
1 2 3 4 5 6 7 8 9 def predict (X ):eval ()2 ).permute(0 , 2 , 1 )for i, row in enumerate (output[0 ]) if row[0 ] != -1 ]return output[0 , idx]
1 2 3 4 5 6 7 8 9 10 11 12 def display (img, output, threshold ):5 , 5 ))for row in output:float (row[1 ])if score < threshold:continue 0 :2 ]2 :6 ] * torch.tensor((w, h, w, h), device=row.device)]'%.2f' % score, 'w' )0.9 )
区域卷积神经网络 R-CNN
R-CNN
思路:
预生成一堆形状、大小不同的候选框,大约 2000 个;
将每个候选框缩放成固定大小,例如 227x227,然后使用预训练的卷积网络(如 AlexNet),从候选框区域提取特征(固定长度的特征向量);
训练支持向量机预测候选框的类别;
根据特征和预测的类别,训练线性回归层,预测与真实边框的偏移;
缺点:
由于每个候选框都需要做前向传播计算,比较费时;
需要分阶段训练,先训练向量机,再训练回归器,比较麻烦;
每个候选框都需要分配内存,内存开销比较大;
Fast R-CNN
思路:
先使用卷积网络生成特征图;
生成候选区域;
将特征图映射到候选区域上,并使用 ROI 兴趣区域池化,得到固定大小的特征向量(输出);
使用全连接层对特征向量进行分类和边界框回归预测;
输出类别和边框;
优点:
速度快,整张图片只需要做一次前向传播进行特征提取,无须每个候选框单独算一次;
准确率高;
内存占用少;
兴趣区域池化示例:
假设输入为 4x4,兴趣区域为 3x3,池化为 2x2,该兴趣区域池化后的结果为:
1 2 3 4 5 6 7 8 9 10 11 12 13 import torchimport torchvision16. ).reshape(1 , 1 , 4 , 4 )0 , 0 , 0 , 20 , 20 ], [0 , 0 , 10 , 30 , 30 ]])2 , 2 ), spatial_scale=0.1 )
1 2 3 4 tensor([[[[ 5., 6.],
Faster R-CNN
Fast R-CNN 仍然生成了大量的候选区域,Faster 的改进在于,不再使用选择性搜索创建候选区域,而是改为生成候选区域网络 region proposal network;
候选区域网络的生成方法很像 SSD,以特征图的像素为中心,生成多个不同尺寸的锚框,预测这些锚框的类别和偏移量,使用极大值抑制去除重复。
这种方法相当于让模型自己学习如何生成候选区域的规则,而不是由我们手动编写规则。
Mask R-CNN
Mask R-CNN 与其他 R-CNN 的区别在于标签不再是锚框,而是像素极的掩码;从而实现了目标的像素级分割功能。
兴趣区域池化 -> 兴趣区域对齐;
额外增加一个全卷积块用于掩码预测;
兴趣区域对齐包括:
分类头:判断 ROL 属于哪个类别
锚框回归:微调 ROL 的位置;
掩码头:为每个 ROL 生成一个二值掩码,用于表示目标实例的轮廓;
语义分割和数据集
图像分割和实例分割
语义分割:识别图像中每一个像素的内容是什么,例如是一只狗,还是一只猫。但不区分多只不同的狗或猫;
实例分割:在语义识别的基础上,区分同一语义的不同实例;
图像分割:将图像划分为不同的区域,划分方法可能跟语义无关,更关是像素之间的特征区分,例如颜色不同;
语义分割数据集
Pascal VOC2012 是一个重要的语义分割数据集
转置卷积
常规卷积模块在下采样的过程中,池化计算会让输出的尺寸减半,有时候这种减半会带来不便。例如如果没有减半,仍然保持和输入相同的形状时,将使得后续的像素级分类变得很方便。转置卷积可用来保持尺寸不变。
基本操作
常规卷积会缩小输入尺寸,而转置卷积通过类似广播的机制,会扩大输入的尺寸;
1 2 3 4 5 6 7 8 9 10 11 12 13 import torchfrom torch import nnfrom d2l import torch as d2ldef trans_conv (X, K ):0 ] + h - 1 , X.shape[1 ] + w - 1 ))for i in range (X.shape[0 ]):for j in range (X.shape[1 ]):return Y
1 2 3 X = torch.tensor([[0.0 , 1.0 ], [2.0 , 3.0 ]])0.0 , 1.0 ], [2.0 , 3.0 ]])
1 2 3 tensor([[ 0., 0., 1.],
填充、步幅和多通道
对于常规卷积,填充提的是对输入进行填充。在转置转移中,填充指的是对输出进行填充。例如填充1,则输出的第一和最后的行和列,将被删除;
1 2 3 tconv = nn.ConvTranspose2d(1 , 1 , kernel_size=2 , padding=1 , bias=False )
1 2 3 4 5 6 7
转置卷积的步幅指的是中间结果的步幅,而不是输入,因此转置卷积的步幅会扩大输出的尺寸:
1 2 3 tconv = nn.ConvTranspose2d(1 , 1 , kernel_size=2 , stride=2 , bias=False )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
对于批量多个输入和多通道,转置卷积和常规卷积计算方式相同,没有差异。
与矩阵变换的关系
常规卷积的前向传播函数通过将输入 X 和权重矩阵相乘来实现:y = Wx
常规卷积的反向传播函数通过将输入与转置的权重矩阵相乘来实现:y =
W T
x
全卷积网络 FCN
全卷积网络使用转置卷积,将特征图的尺寸重新转成输入图像的尺寸,从而实现了逐像素级别的分类预测。中间还使用了一个 1x1 的卷积层,将通道数转成类别个数。
构造模型
1 2 3 4 5 import torchimport torchvisionfrom torch import nnfrom torch.nn import functional as Ffrom d2l import torch as d2l
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 True )list (pretrained_net.children())[-3 :]list (pretrained_net.children())[:-2 ])1 , 3 , 320 , 480 ))21 'final_conv' , nn.Conv2d(512 , num_classes, kernel_size=1 ))'transpose_conv' , nn.ConvTranspose2d(num_classes, num_classes,64 , padding=16 , stride=32 ))
初始化转置卷积层
上采样可使用双线性插值法,以初始化转置卷积层。
双线性插值法:
根据输出的坐标 (
x
,
y
),计算在输入图像上的映射坐标 (
x ′
,
y ′
)
在输入图像上找到离 (
x ′
,
y ′
) 坐标最近的 4 个像素;
输出图像上在 (
x
,
y
) 的像素值可根据这 4 个像素和 (
x ′
,
y ′
) 的相对距离进行估算;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def bilinear_kernel (in_channels, out_channels, kernel_size ):1 ) // 2 if kernel_size % 2 == 1 :1 else :0.5 1 , 1 ),1 , -1 ))1 - torch.abs (og[0 ] - center) / factor) * \1 - torch.abs (og[1 ] - center) / factor)range (in_channels), range (out_channels), :, :] = filtreturn weight3 , 3 , kernel_size=4 , padding=1 , stride=2 ,False )3 , 3 , 4 ));
1 2 3 4 img = torchvision.transforms.ToTensor()(d2l.Image.open ('../img/catdog.jpg' ))0 ) 0 ].permute(1 , 2 , 0 ).detach()
1 2 3 4 5 d2l.set_figsize()print ('input image shape:' , img.permute(1 , 2 , 0 ).shape)1 , 2 , 0 ));print ('output image shape:' , out_img.shape)
1 2 input image shape: torch.Size([561, 728, 3])
1 2 3 64 )
读取数据集
1 2 batch_size, crop_size = 32 , (320 , 480 )
1 2 read 1114 examplesread 1078 examples
训练
1 2 3 4 5 6 def loss (inputs, targets ):return F.cross_entropy(inputs, targets, reduction='none' ).mean(1 ).mean(1 )5 , 0.001 , 1e-3 , d2l.try_all_gpus()
1 2 loss 0.443, train acc 0.863, test acc 0.852type ='cuda' , index=0), device(type ='cuda' , index=1)]
预测
1 2 3 4 5 6 7 8 9 10 11 def predict (img ):0 )0 ])).argmax(dim=1 )return pred.reshape(pred.shape[1 ], pred.shape[2 ])def label2image (pred ):0 ])return colormap[X, :]
在输入图像的尺寸无法被 32 整除时,可将输入图像按 32 倍数的尺寸裁剪成多个子图像,以便每个子图像的尺寸都能够被 32 整除。每个子图像单独预测,最后将它们拼接在一起,重叠的像素有多个值,这些值拼接后使用 softmax 预测类别。
1 2 3 4 5 6 7 8 9 10 voc_dir = d2l.download_extract('voc2012' , 'VOCdevkit/VOC2012' )False )4 , []for i in range (n):0 , 0 , 320 , 480 )1 ,2 ,0 ), pred.cpu(),1 ,2 ,0 )]3 ] + imgs[1 ::3 ] + imgs[2 ::3 ], 3 , n, scale=2 );
优点:
支持任意尺寸输入;
端到端训练,不用额外的后处理;
可复用现有的特征提取网络,例如VGG、ResNet,迁移效率高;
缺点:
对小目标或细长目标的分类效果不好;
分割边界不够精确(相比 U-net、DeepLab 等);
上采样丢失了一些细节;
全连接层是线性回归算法,因此它要求输入的维度和它的参数维度是匹配的,这样才能够完成全连接的计算。这也导致了凡是输出层采用全连接层的网络模型,都无法支持任意尺寸的输入。FCN 由于放弃了全连接层,改用全卷积层,因此 FCN 才能够支持任意尺寸的输入。对于卷积层来说,它只有卷积核的参数是固定,然后是滑动计算的。跟全连接层的线性回归很不一样。
风格迁移
方法
原理:从两张输入的图像中,各提取一部分特征,作为目标图像的新特征,然后组成这些新特征,更新目标图像;
实现原理:
使用多层特征提取网络,分别从输入的两张图像(内容图像、风格图像)中,提取每一层的特征;
初始化目标图像为内容图像,同样使用多层网络从中提取特征。此时它的特征跟内容图像相同;
计算目标图像和风格图像的某一层的损失,反向传播迭代风格参数;不断更新合成图像的参数;
阅读内容和风格图像
1 2 3 4 5 6 7 8 import torchimport torchvisionfrom torch import nnfrom d2l import torch as d2lopen ('../img/rainier.jpg' )
1 2 style_img = d2l.Image.open ('../img/autumn-oak.jpg' )
预处理和后处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 rgb_mean = torch.tensor([0.485 , 0.456 , 0.406 ])0.229 , 0.224 , 0.225 ])def preprocess (img, image_shape ):return transforms(img).unsqueeze(0 )def postprocess (img ):0 ].to(rgb_std.device)1 , 2 , 0 ) * rgb_std + rgb_mean, 0 , 1 )return torchvision.transforms.ToPILImage()(img.permute(2 , 0 , 1 ))
抽取图像特征
1 2 3 4 5 6 7 8 9 pretrained_net = torchvision.models.vgg19(pretrained=True )0 , 5 , 10 , 19 , 28 ], [25 ]for i in range (max (content_layers + style_layers) + 1 )])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def extract_features (X, content_layers, style_layers ):for i in range (len (net)):if i in style_layers:if i in content_layers:return contents, stylesdef get_contents (image_shape, device ):return content_X, contents_Ydef get_styles (image_shape, device ):return style_X, styles_Y
定义损失函数
内容损失
1 2 3 4 def content_loss (Y_hat, Y ):return torch.square(Y_hat - Y.detach()).mean()
风格损失
1 2 3 4 5 6 7 8 9 def gram (X ):1 ], X.numel() // X.shape[1 ]return torch.matmul(X, X.T) / (num_channels * n)def style_loss (Y_hat, gram_Y ):return torch.square(gram(Y_hat) - gram_Y.detach()).mean()
全变分损失
高频噪点:特别亮或特别暗的颗粒像素。
全变分去噪法:和隔离的像素平均一下
∑ i , j | x i , j − x i + 1 , j | + | x i , j − x i , j + 1 |
1 2 3 def tv_loss (Y_hat ):return 0.5 * (torch.abs (Y_hat[:, :, 1 :, :] - Y_hat[:, :, :-1 , :]).mean() +abs (Y_hat[:, :, :, 1 :] - Y_hat[:, :, :, :-1 ]).mean())
损失函数
总损失由内容损失、风格损失、全变分损失三个损失进行加权求和。至于每个损失的权重多少,则看更看重哪个。
1 2 3 4 5 6 7 8 9 10 11 12 content_weight, style_weight, tv_weight = 1 , 1e3 , 10 def compute_loss (X, contents_Y_hat, styles_Y_hat, contents_Y, styles_Y_gram ):for Y_hat, Y in zip (for Y_hat, Y in zip (sum (10 * styles_l + contents_l + [tv_l])return contents_l, styles_l, tv_l, l
初始化合成图像
1 2 3 4 5 6 7 8 9 class SynthesizedImage (nn.Module):def __init__ (self, img_shape, **kwargs ):super (SynthesizedImage, self ).__init__(**kwargs)self .weight = nn.Parameter(torch.rand(*img_shape)) def forward (self ):return self .weight
1 2 3 4 5 6 def get_inits (X, device, lr, styles_Y ):for Y in styles_Y]return gen_img(), styles_Y_gram, trainer
训练模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def train (X, contents_Y, styles_Y, device, lr, num_epochs, lr_decay_epoch ):0.8 ) 'epoch' , ylabel='loss' ,10 , num_epochs],'content' , 'style' , 'TV' ],2 , figsize=(7 , 2.5 ))for epoch in range (num_epochs):if (epoch + 1 ) % 10 == 0 :1 ].imshow(postprocess(X))1 , [float (sum (contents_l)),float (sum (styles_l)), float (tv_l)])return X
1 2 3 4 5 device, image_shape = d2l.try_gpu(), (300 , 450 )0.3 , 500 , 50 )